Depth First Search-Artificial intelligence:

Depth first search is  similar to breadth first, except that things are added to the top of the plan rather than the bottom. In our example, the first 3 things o n the agenda would still be:

Hence, once the 'D' state had been searched , the actions:

1. (empty, add'N')

2. (empty, add'D')

3. (empty, add 'A')

Would be added to the top of the plan, so it would look like this:

4. ('D', add 'D')

5. ('D', add 'A')

6. ('D', add 'N')

Certainly, carrying out the action at the top of the plan  would introduce the string 'DD', but then this would cause the action:

('DD', add 'D')

to be added to the top, and the next string searched  would be 'DDD'. Obviously, this can go on definitely, and in practice, we might specify a depth bound to stop it going down a particular path forever. That is, our agent will have  to record how far down a specific  path it has gone, and avoid putting actions on the plan if the state in the agenda item is past a certain

Notice that our search for names is special: no matter what state we reach, there will always be 3 actions to put to the plan. In other searches, the number of actions available to undertake on a particular state may be 0 that effectively stops that branch of the search. perhaps, a depth limit is not always required.

Back to our example, if the professor stipulated that she wanted very short names (of three or fewer letters), then the search tree would appear like this.

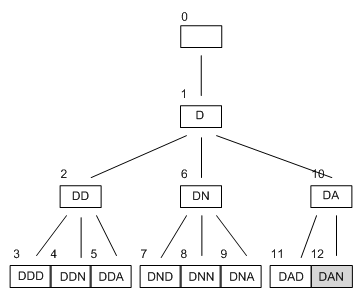
We see that 'DAN' has been reached after the 12th step, so there is an improvement on the breadth first search. Whether, in this case, it was fortunate that the first letter explored is 'D' and that there is a solution at depth 3. If the depth limit had been set at four  instead, the tree would have looked very  different.

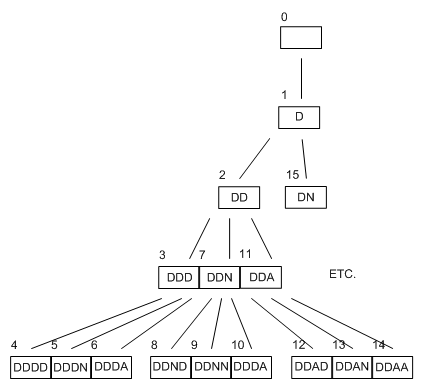
It seem like it will be a long time until it finds 'DAN'. This highlights an essential drawback to depth first search. It may often go deep down paths which have no solutions, when there is a solution much higher up the tree, but on a another branch. Also depth first search is not complete, in general.

Rather than just adding the next planed  item directly to the top of the agenda, it might be a good  idea to make sure that every and each  node in the tree is fully expanded before moving on to the following  depth in the search. This is the kind of depth first search which and Norvig and Russell's explain. For our DNA example, if we did this, the search tree would seem like this:

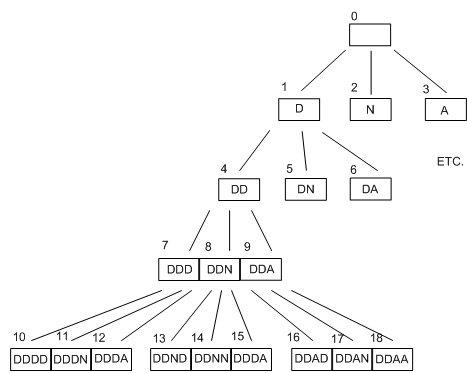
The great advantage to depth first search is that it requires much less memory to operate than breadth first search. If we count the number of 'alive' nodes in the above diagram, it amounts to only four, because the ones on the bottom row are not to be expanded due to the depth boundary Indeed, it may be shown that if an agent wants to find  for all solutions up to a depth of d in a space with branching factor b, then in a depth first search it only have  to remember up to a utmost of d*b states at any 1 time.

To put this in perspective, if our professor wanted to find  for every  names up to length eight , she would  have to remember 8*3 = 24 different strings to complete a depth first search (rather than 2187 in a breadth first search).