Deflection at the centre:
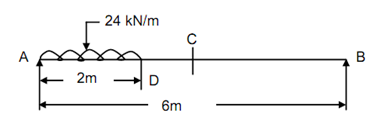
A simply supported beam of span 6 m is subjected to Udl of 24 kN/m for a length of 2 m from left support. Discover the deflection at the centre, maximum deflection & slopes at the ends and at the centre. Take EI = 20 × 106 N-m2.
Solution
∑ Fy = 0, so that RA + RB = 24 × 2 = 48 kN --------- (1)
Taking moments around A,
24 × 2 × 1 = RB × 6
RB = 8 kN (↑) -------- (2)
RA = 48 - 8 = 40 kN (↑). ------------(3)
By apply the Udl over the portion DB downwards and upwards,
Figure
M = 40 x - 24 x × (x/2) + 24 ( x - 2) ( (x - 2)/2)
Note down that the third term vanishes if x < 2 m.
= 40 x - 12 x2 + 12 ( x - 2)2 ------- (4)
EI d 2 y/ dx2 = 40 x - 12 x 2 + 12 ( x - 2)2 ------- (5)
EI dy / dx = 40 x2/2- 12 x3 /3+ 12 ( x - 2)3/3 + C1
= 20 x2 - 4 x3 + 4 ( x - 2)3 + C1 -------- (6)
EIy = 20 x 2/3 - x4 + (x - 2)4 + C1 x + C2 -------- (7)
Here again note that the third term vanishes for x < 2 m.
at A, x = 0, y = 0 ∴ C2 = 0
at B, x = 6 m, y = 0
0 = 20 × 63 /3 - 64 + (6 - 2)4 + C1 × 6
C1 =- 20 × 12 + 36 × 6 - ((16 × 16 )/6)=- 200/3
∴ EI dy/dx = 20 x2 - 4 x3 + 4 ( x - 2)3 - 200/3 -------- (8)
The third term vanishes.
Slope at A, (x = 0), 27
θA = -200/3EI =- (200 × 103)/ (3 × 20 ×106)
= -(1/300) rad = - 3.33 × 10- 3 rad
Slope at B, (x = 6 m),
EI θ B = 200 × 62 - 4 × 63 + 4 (6 - 2)3 - (200/3)
θ = 136/ 3 EI = (136 × 103 )/(3 × 20 ×106)
= + 2.27 × 10- 3 radian
Slope at C, (x = 3 m), i.e. x > 2 m
EI θ C = 20 × 32 - 4 × 33 + 4 (3 - 2)3 - (200/3)
θC = 20 /3 EI = 0.47 × 10- 3 radians
EIy =( 20 x 3/3)- x4 + ( x - 2)4 - (200/3) x -------- (9)
Deflection at centre, (x = 3 m),
EIyC = (20/3) × 33 - 34 + (3 - 2)4 - (200 /3)× 3
yC = - 100 / EI = - 100 × 103 × 103 / (20 × 106)
= - 5 mm
For maximum deflection,
dy/ dx = 0
0 = 20 x2 - 4x3 + 4 ( x - 2)3 - (200/3)
= 20 x2 - 4x3 + 4x3 - 32 - 24 x2 + 48 x - (200 /3)
=- 4x2 + 48 x - (296 /3)
∴ x2 - 12x + (74 /3 )= 0
x = 2.63 m , x > 2m
EIy max = (20/3) × 2.633 - 2.634 + (2.63 - 2)4 - (200/3) × 2.63 = - 101.7
∴ ymax = - 5.087 mm; - 5.1 mm