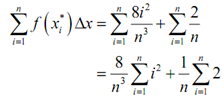Using the definition of the definite integral calculate the following.

                                                            ∫₀²  x²  + 1dx

Solution

Firstly, we can't in fact use the definition unless we find out which points in each interval that well use for x_i* .  To make our life simple we'll utilizes the right endpoints of each interval.

We know that for general n the width of each subinterval is,

Δx = 2 - 0/n = 2/n

The subintervals are then,

 [0,  2/n] , [2/n ,  4/n ]  [ 4/n   6/n] .......[ 2 (i -1)/n ,2i/n],...,[2(n-1)/n , 2]

Since we can see the right endpoint of the i^th subinterval is

                                             x _i *  = 2i/n

The summation in the definition of the definite integral is then,

Now, we have to take a limit of this. That means that we need to "evaluate" this summation..

In order to do this we will have to recognize that n is a constant so far as the summation notation is concerned. Since we cycle through the integers from 1 to n in the summation only i changes & therefore anything that isn't an i will be a constant and can be factored out of the summation.  In specific any n that is in the summation can be factored out if we have to.

Following is the summation "evaluation".

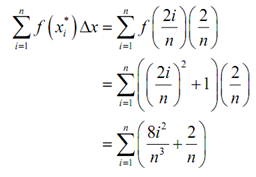
=8/n³ (( n ( n + 1) ( 2n + 1) )/6 )+(1/n) (2n )

= (4 ( n + 1) ( 2n + 1))/3n² )+ 2)

= (14n² + 12n + 4)/3n2

Now we can determine the definite integral.

                    =14/3