Definition of limit : Consider that the limit of f(x) is L as x approaches a & write this as

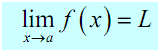
provided we can make f(x) as close to L as we desire for all x adequately close to a, from both sides, without in fact letting x be a.

Well let's assume that we know that the limit does actually exist.  According to our "working" definition then we can decide how close to L that we'd like to make f(x).  For sake of argument let's assume that we desire to make f(x) no more that 0.001 away from L.  It means that we desire one of the following

f ( x ) - L < 0.001       if f ( x ) is larger than L

L - f ( x ) < 0.001       if f ( x ) is smaller than L

Now according to the "working" definition it means that if we get x adequately close to a we can make one of the above true.  Though, actually it says a little more. Actually It says that somewhere out there in the world is a value of x, say X, so that for all x's which are closer to a than X then one of the above statements will be true.

It is actually a fairly significant idea. There are several functions out there in the world which we can make as close to L for particular values of x that are close to a, however there will be other values of x near to a that give functions values which are nowhere near close to L.  In order for a limit to present once we get f(x) as close to L as we desire for some x then it will need to stay in that close to L (or get closer) for all values of x that are closer to a.

In rather simpler terms the definition says that as x gets closer & closer to x=a (from both sides of course...) then f(x) have to be getting closer & closer to L.  Or, as we move in towards x=a then f(x) have to be moving in towards L.

It is significant to note once again that we have to look at values of x that are on both sides of x=a. We have to also note that we are not permitted to use x=a in the definition.  We will frequently use the information which limits give us to get some information regarding what is going on right at x=a, however the limit itself is not concerned  along with what is in fact going on at x=a. The limit is just concerned with what is going on around the point x=a.  it is an important concept regarding limits that we have to keep in mind.

An alternative notation that we will occasionally use in denoting limits is

f ( x) → L        as             x → a