Infinite limits : Let's now move onto the definition of infinite limits. Here are the two definitions which we have to cover both possibilities, limits which are positive infinity & limits which are negative infinity.

Definition: Let f(x) be a function described on an interval which contains x = a , except possibly at x = a .  Then we say that,

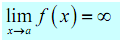
if for each number M > 0 there is some number δ > 0 such that

f ( x ) > M           whenever     0 <|x-a|< δ

Definition:  Let f(x) be a function described on an interval which contains x = a , except probably at x = a .  Then we say that,

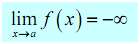
if for every number N < 0 there is some number δ > 0 such that

f ( x )< N whenever    0 <|x-a|< δ

Note that in these two definitions M has to be a positive number and that N has to be a negative number.  That's a simple distinction to miss if you aren't paying close attention.

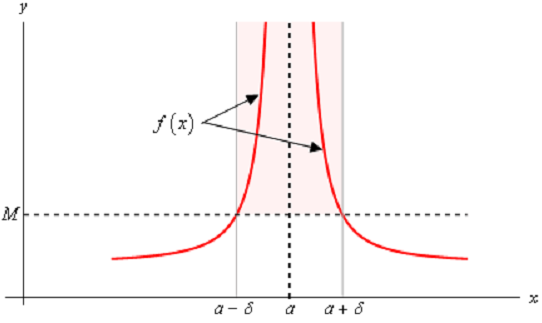
Also note as well that we could also write down definitions for one-sided limits which are infinity if we desired to. We'll leave that up to you to do if you'd like to. Following is a quick sketch illustrating Definition.

Let's work on example of one of these to illustrate how these differ from the previous examples.