Define the Gauss Seidel Method

The Gauss-Seidel method is an iterative method in which the voltage of each node is calculated in turn using the most up to date voltages for the other nodes. The voltage calculated is that which gives the correct solution for the node considered, based upon the data specified and the previously calculated voltages of the other nodes. The method is equally applicable to both a.c. and d.c. circuits.

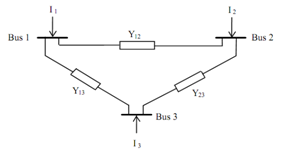
Consider the three busbar system shown in Figure.

Using Nodal analysis, the current fed into each bus is given as:

 I₁  =  Y₁₁ V₁ + Y₁₂ V₂ + Y₁₃ V₃             

 I₂  =  Y₂₁ V₁ + Y₂₂ V₂ + Y₂₃ V₃     

 I₃  =  Y₃₁ V₁ + Y₃₂ V₂ + Y₃₃ V₃             

or,  in matrix form,

  [I] = [Y] [V]

where Y_nn is node n self admittance (sum of all the admittances connected to node n).

 Y_nm is the mutual admittance between nodes n and m (sum of the admittances connecting node n to node m)

Note that:  (i) all mutual admittance terms have a negative sign,

  (ii) all injected currents are positive.

Recalling that  S  =  P + j Q  =  V I *

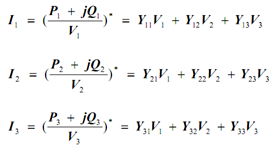
In general, for an n busbar system, the current fed into busbar k is given as:

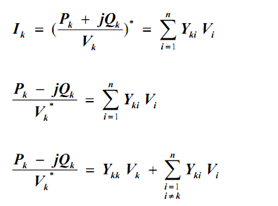
Therefore, the voltage at busbar k is given as:

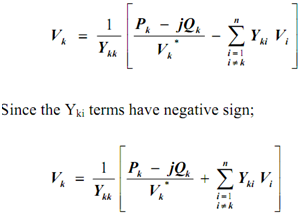
Where V_k and V_i are the voltages at nodes 'k' and 'i', respectively,

  Y_kk  is node 'k' self admittance,

Y_ki   is the mutual admittance between nodes 'k' and 'i',

 P_k - jQ_k  is the total power flowing into node 'k'.