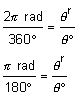Q. Define Degrees and Radians?
Ans.
Just as your height can be measured in meters or feet and your weight can be measured in pounds or kilograms, angles can be measured in degrees or radians. Radian angle measurements are used a great deal in calculus.
A degree is the measure of the angle formed by dividing a complete revolution by 360.
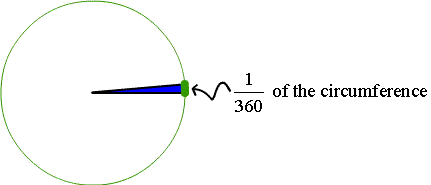
There are 360 degrees, written 360o, in a circle.
The arclength is the length of part of the circumference of the circle.

A radian is the measure of the angle which defines a sector with arclength equal to the radius of the circle. We use rad as a symbol for radian.
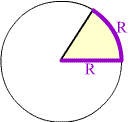
There are 2p radians in a circle.
The circumference of a circle of radius is 2Πr, thus the circumference of the unit circle (a circle with radius 1, centered at the origin) is 2Π. Since the radius of the unit circle is equal to 1, there are 2Π radians in the whole circle.
These diagrams compare radians with degrees.
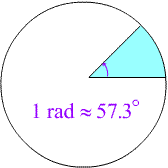
There are 2p radians in a circle and 360o in a circle. So we can use the following proportion to convert between degree and radian measurements.
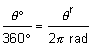
where
θo represents the measure of the angle in degrees
θr represents the measure of the angle in radians
We can simplify this equation as follows: