Cumulative distribution function - Poisson distribution:

Find the cdf of Y = X₁, + X₂ where X_I and X₂ independently follow Poisson distribution with parameters λ_l and λ₂ respectively.

Solution:

The cdf of Y is

F(y) =P(Y≤ y) =P (X₁ + X₂ ≤ y)

= ∑ ∑ e ^{- λ1} λ₁ ^x1/x1!  e^{- λ2} λ₂^x2

x₁+x₂ ≤  y

The summation is taken over all integer values of ( x_l, x₂ ) satisfying x_l ≥ 0, x₂ ≥ 0, x₁ + x₂ ≤ y . Making the substitution r = x_l + x₂, x₁ = x We have x_l = x, x₂, = r-x.

Thus, region of summation in terms of r, x is all integers (x, r ) satisfying

x ≥ 0 , r - x ≥ 0, r ≤ y

or

0 ≤ x ≤ r ≤ y

Writing the summation in terms oi r and x, rearranging the terms, we have

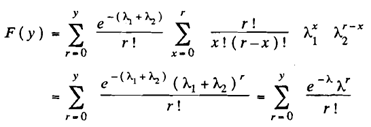
where λ = λ _l + λ₂ . The final expression of F (y) is the cdf of Poisson distribution with parameter λ. Hence Y also follows a Poisson distribution with parameter λ.