Convert each of the following points into the specified coordinate system.

 (a) (-4, 2 Π /3) into Cartesian coordinates.

(b) (-1,-1) into polar coordinates. 

Solution

(a) transform (-4, 2 Π /3) into Cartesian coordinates.

This conversion is very easy.  All we require to do is plug the points into the formulas.

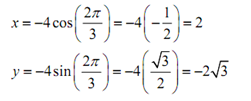
So, in Cartesian coordinates this point is (2, -2  3).

(b) Convert or transform (-1,-1) into polar coordinates.

 Let's first get r.

r = √(-1)² + (-1)²

= √2

Now, let's get θ.

θ = tan^-1 (-1/-1)

= tan^-1 (1) = Π/4

Though this is not the correct angle, this value of θ is in the first quadrant and the point we have been specified is in the third quadrant.  As noted above we can obtain the correct angle by adding π onto this.  Hence, the actual angle is,

θ = Π/4 + Π = 5Π /4

So, in polar coordinates the point is  (√2, 5π/4). Note also that we could have utilized the first θ that we got by using a negative r.  In this type of case the point could as well be written in polar coordinates

as  (-√2, π/4).