Conclude the values of the six trigonometric functions:

Conclude the values of the six trigonometric functions of an angle formed through the x-axis and a line connecting the origin and the point (3,4).

Solution:

For help to "see" the solution of the problem it helps to plot the points and construct the right triangle.

Label all the known angles and sides, as display in Figure.

From the triangle, we can see that two of the sides are given. But to answer the problem, all three sides must be determined. Thus the Pythagorean Theorem must be applied to solve for the unknown side of the triangle.

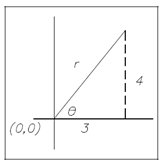
Figure:  Example Problem

x = 3

y = 4

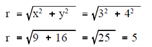
Having solved for all three sides of the triangle, the trigonometric functions can now be conclude.  Substitute the values for x, y, and r within the trigonometric functions and solve.

Sin Θ = y/r = 4/5 = 0.800

Cos Θ = x/r = 3/5 = 0.600

Tan Θ = y/x = 4/3 = 1.333

Csc Θ = r/y  =5/4 = 1.250

Sec Θ = r/x = 5/3 = 1.667

Cot Θ = x/y = 3/4 = 0.750

While the trigonometric  functions of angles are described in terms of lengths of the sides of right  triangles,  they  are  actually  functions  of  the  angles  only.  The numerical values of trigonometric functions of any angle depend on the size of the angle and not on the length of the sides of the angle.   Therefore, the sine of a 30   angle is always 1/2 or 0.500.