Compute the thermal stresses in steel:

Consider the compound bar shown in below figure consisting of a steel bolt of diameter 18 mm, surrounded through a copper tube of outer and inner diameters 30 mm and 18 mm respectively. The assembly is just snug at 15^oC. The material properties are given as:

Young's modulus of steel, E_S = 200 kN/mm²

Young's modulus of copper, E_C = 120 kN/mm².

Coefficient of linear thermal expansion of steel, α_s  = 12 × 10^-6  m/m/ ^o C

Coefficient of linear thermal expansion of copper, α_c  = 18 × 10^-6  m/m/ ^o C

Compute the thermal stresses in steel and copper when the temperature of the assembly is raised to 45^oC.

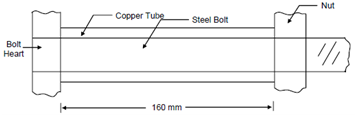
Figure

Solution

In this case, when the temperature of the assembly is raised, copper will expand more than steel and hence, will exert a thrust on the steel nut and bolt head thus producing tension in the steel. Since there is no other external force this tension has to be kept in equilibrium by the compressive force induced in copper. Hence by formulating a compatibility condition of total strains (thermal + elastic) the problem could be solved.

Now let the forces induced in steel and copper are designated as P_s and P_c respectively in kN units.

Thermal strain in steel, ε_st  = α_s  × ΔT

= 12 × 10^-6 × (40 - 15)

= 3 × 10^-4 m/m

Thermal strain in copper, α_c  × ΔT

= 18 × 10^-6 × (40 - 15)

= 4.5 × 10^-4 m/m

Elastic strain in steel,  δ_se  = P_s /A_s E_s

=          P_s/ (π/4) × 18² × 200

= 1.965 × 10^-5 Ps

Elastic strain in copper, δ_ce = P_c /A_c E_c

=          P_c/ (π/4) × (30² - 18²) 120

= 1.8421 × 10^-5 Pc