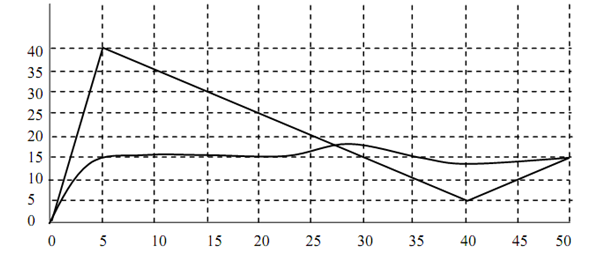
An animation demonstrates a car driving along a road that is given by a Bezier curve along with the subsequent control points: 

The animation finals 10 seconds and the key frames are to be calculated at 1 second intervals. Compute the position of the car on the road at the beginning of the 6^th second of the animation.

Solution: By using similar process in the previous exercise we can compute the blending functions as:

1.   B₀₃ = 3!/(0! x (3-0)!) u⁰(1 - u)^(3-0) = 1u⁰(1 - u)³ = (1 - u)³

2.   B₁₃ = 3!/(1! x (3-1)!) u¹(1 - u)^(3-1) = 3u¹(1 - u)² = 3u(1 - u)²

3.   B₂₃ = 3!/(2! x (3-2)!) u²(1 - u)^(3-2) = 3u²(1 - u)¹ = 3u²(1 - u)

4.   B₃₃ = 3!/(3! x (3-3)!) u³(1 - u)^(3-3) = 1u³(1 - u)⁰ = u³

The function x(u) is equivalent to x(u) =   ∑x_kB_k; here k=0,1,2,3

x(u)       = ∑ x_kB_k =  x₀B₀₃   +   x₁B₁₃ + x₂B₂₃ +  x₂B₃₃

=  (0)(1  -  u)³    +  5  [3u(1  -  u)²]  +  40  [3u²(1  -  u)]  +  50  u³

= 15u(1 - u)² + 120u²(1 - u) + 50u³

As the same y(u) = y₀B₀₃ + y₁B₁₃+ y₂B₂₃+  y₂B₃₃

=  (0)(1  -  u)³    +  40  [3u(1  -  u)²]  +  5  [3u²(1  -  u)]  +  15  u³

= 120u(1 - u)² + 15u²(1 - u) + 15u³

At the beginning of the sixth second of the animation, that is, when u=0.6, we can utilize these equations to work out such x(0.6) = 29.52 and y(0.6) = 16.92.

The way of the car looks like as: