Compute depth of yielding in the hollow shaft:

A solid shaft 80 mm diameter is solid for a certain length from one end but hollow for the remaining length along inner diameter of 40 mm. If a pure torsion is applied such that yielding occur at the surface of the solid part of the shaft. Compute:

 (1) the depth of yielding in the hollow shaft, and

 (2) the ratio of the angles of twist per unit length.

Solution

τ = Shear stress at yield point.

Torsion in the solid shaft =τ × ( π× 80³ /16)

T₁ =τ × (π× 80³ /16)            ------------- (1)

 For Hollow Shaft

Torsion in the unyielded part

T₂ =τ × (π/16 D) (D ⁴ - 40⁴)                    ----------- (2)

where D = diameter of the hollow section at which yielding begins.

Torsion in yielded part

= (πτ /12 )(80³  - D³ ) --------------  (3)

         T₁  = T₂  + T₃

⇒ 80³/16 = D4  - 40⁴/16 D +  (80³ - D³/12)

⇒         12 × 80³ D = ( D⁴  - 40⁴ ) 12 + 16 D (80³  - D³ )

⇒         6144 × 10³ D = 12D⁴  - 3072 × 10⁴  + 8192 × 10³ D - 16 D⁴

⇒         4D⁴  - 2048 × 10³ D + 3072 × 10⁴  = 0

⇒         D ⁴  - 512 × 10³ D + 768 × 10⁴  = 0           ----------- (4)

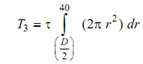
By trial and error, D = 74.8 mm

T / J =  τ/ R = G θ/ l

⇒         θ=  τl /GR                                 ---------- (5)

θ_S  =2τl / (G × 80)            ------ (6)

θ_H  = 2τl / (G × D)           --------- (7)

θ_H/ θ_S  = 80/ D =   80/74.5 = 1.07