Complex Numbers

In the radicals section we noted that we won't get a real number out of a square root of a negative number.  For example √-9 isn't a real number as there is no real number which we can square & get -ve  9.

We now also saw that if a and b were both positive then √(ab) = √a√b .For a second let's forget that limitation and do the following.

√-9 =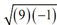 = √9 √ -1 = 3 √-1

 Now, √-1 is not a real number, however if you think about it we can do this for any square root of a negative number.  For example,

√-100 =√100√-1=10√-1

√-5=√5√-1

√-290=√290√-1 etc.

Thus, even if the number isn't a perfect square still we can always reduce the square root of a -ve number down to the square root of a +ve number (which we or a calculator can deal with) times √-1 .

Thus, if we only had a way to deal with √-1 we could really deal with square roots of negative numbers.  Well the reality is that, at this level, there only isn't any way to deal with

√-1. Thus rather than dealing with it we will "make it go away" so to speak using the following definition.

                                               i =√-1

Note that if we square both of sides of this we get,

                                             i²  = -1

It will be significant to remember this later on. It shows that, in some way, i is the only "number" which we can square and acquire a negative value.

By using this definition all the square roots above become,

√-9 = 3i                              √-100=10i

√-5=√5i                              √-290 = √290 i

These all are examples of complex numbers.