Now we take up combinations and its related concepts. Combinations are defined as each of the groups or selections which can be made by taking some or all of the elements from the given elements. The combinations of taking two units out of four units is given by

         AB, AC, AD, BC, BD, CD

That is, in combinations the emphasis on order is not there and one is concerned with only the number of units that ought to be selected.

Finding the number of combinations of 'n' dissimilar things taken 'r' at a time:

To obtain this relationship, we consider a set S consisting of n elements which are distinct. To specify a permutation of size 'r' chosen from these 'n' elements, we can first select the r elements that will appear in the permutation, and then we can give the order in which the selected elements are to be arranged. Here in this case, the first step constitutes the selection of a combination of 'r' elements from set 'S' consisting of 'n' elements, and this can be done in  ⁿC_r  ways. The second step constitutes the arrangement of these elements. The ordering (arrangement) of these 'r' elements can be accomplished in r! ways. Therefore, the number of permutations of 'n' things taken 'r' at a time, that is ⁿP_r , will be the product of  ⁿC_r and r!. That is,

ⁿP_r  =  ⁿC_r  . r!. This can also be expressed as

ⁿC_r  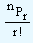=    which gives our required relationship. Since  ⁿP_r  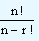=    , the

expression for   ⁿC_r   will be    .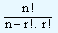

Now we look at a couple of examples.

Example 1.6.6

Find the number of combinations of 50 things taking 46 at a time.

That is, we have to select 46 things out of 50 things without giving any importance to their arrangement. That will be 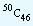   . But we know that

ⁿC_r =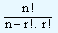 

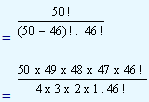
       =  2,30,300.