1. The coil remaining stationary with respect to the flux, the flux varies in magnitude with time. Since no motion is involved, no energy conversion takes place. Equation gives the transformer emf (or the pulsational emf ) as in the case of a transformer, in which a time-varying flux linking a stationary coil yields a time-varying voltage.
2. The flux remaining constant, the coil moves through it. A conductor or a coil moving through a magnetic field will have an induced voltage, known as the motional emf (or speed emf ), given by
Motional emf e = BlU
which is often called the cutting-of-flux equation, where B is the flux density of a non- time-varying, uniform magnetic field, l is the length of the conductor, U is the velocity of the conductor, and ¯B, ¯l, and ¯U are mutually perpendicular in their directions. If the motion is rotary in nature, it is also known as rotational voltage. The direction for the motional emf can be worked out from the right-hand rule: if the thumb, first, and second fingers of the right hand are extended so that they are mutually perpendicular to each other, and if the thumb represents the direction of ¯U and the first finger the direction of ¯B, the second finger will then represent the direction of the emf along ¯l.
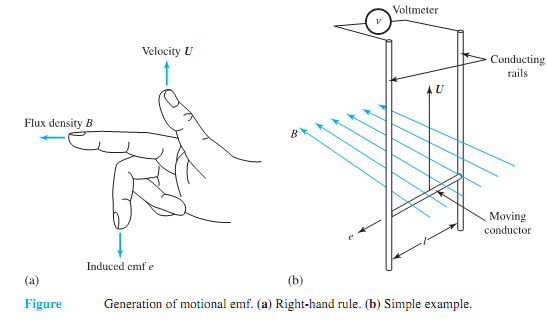
The generation of motional emf is further illustrated by a simple example, where a single-turn coil formed by the moving (or sliding) conductor (moving with velocity U), the two conducting rails, and the voltmeter are situated in a magnetic field of flux density B. The conductor moving with a velocity U, in a direction at right angles to both B and l, sweeps the area lU in 1 second. The flux per unit time in this area is BlU, which is also the flux linkage per unit time with the single-turn coil. Thus, the induced emf e is simply given by BlU. The motional emf (or speed emf) is always associated with the conversion of energy between the mechanical and electrical forms.
3. The coil may move through a time-varying flux; that is to say, both changes (1) and (2) may occur together.Usually one of the two phenomena is so predominant in a given device that the other may be neglected for the purposes of analysis.