Center of Mass - Applications of integrals

In this part we are going to find out the center of mass or centroid of a thin plate along with uniform density ρ. The center of mass or also centroid of a region is the point where the region will be perfectly balanced horizontally whether suspended from that point.

Thus, let's assume that the plate is the region bounded by the two curves f(x) and g(x) on the interval [a,b]. Thus, we wish to find the center of mass of the region below.

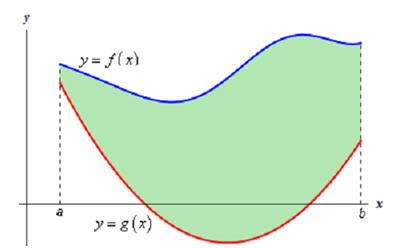
We'll first require the mass of this plate. The mass is,

M = ρ (area of plate)

= ρ ∫^b_a f (x) - g (x) dx

Next we'll require the moments of the region. There are two types of moments, represent by M_x and M_y. The moments calculate the tendency of the region to rotate about the x and y-axis correspondingly. The moments are illustrated by,

Equations of Moments

M_x= ρ ∫^b_a ½([f (x)]² - [g (x)]²) dx

M_y = ρ ∫^b_a x (f (x) - g (x)) dx

After that the coordinates of the center of mass, (?x,? y) are as follow:

Center of Mass Coordinates

X‾ = M_y / M = ∫^b_a x(f (x) - g(x)) dx / ∫^b_a f (x) - g (x)) dx

= 1/A ∫^b_a x (f (x) - g (x)) dx

y‾ = M_x / M = ∫^b_a 1/2 ([f (x)]² - [g(x)]²) dx / ∫^b_a f (x) - g (x)) dx

= 1/A ∫^b_a ½ ([f (x)]² - [g (x)]²) dx

Where

A = ∫^b_a f (x) - g (x) dx