It is a well known fact that the value of a financial claim reflects the present value of the cash flows produced by the financial claim. While valuing an MBS an important thing to be decided upon is with regard to the cash flows, given the nature of the underlying mortgage contracts.
To an MBS investor, cash flows comprises three components,
CFt = NIt + SPt + PRt
Where,
CFt = total cash flow to investor.
NIt = monthly interest payment net of servicing and other fees.
SPt = scheduled principal payment for month t.
PRt = forecasted unscheduled principal repayments in month t (prepayments).
The significant amount is the prepayment PRt, which occurs at the discretion of the borrowers.
The following table shows the mechanics of a classical pass through MBS.
Table
|
Payments of mortgage borrower: PRt + SPt + It
|
|
Repayments: PRt + SPt
|
(Gross) Interest coupon payments: It = i MBt-1
|
|
Forecasted unscheduled prepayment: PRt
|
Monthly scheduled payment of borrowers
(coupon plus amortization on mortgage balance)
MPt = MBt-1 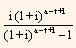
|
|
Prepayments
PRt = SMMt (MBt-1) - SPt)
|
Scheduled repayments
SPt = MPt - It
|
Interest net of service fees
NLt = MBt-1 (i - s)
|
Service fee (going to servicer)
St = s MBt-1
|
|
Cash flow to MBS investors: CFt = PRt + SPt + It - St = PRt + SPt + NIt
|
|
Where,
It = Gross interest coupon payments
MBt = Mortgage balance
MPt = Monthly scheduled payment of borrowers
SMMt = Standard monthly mortality rate, i.e. prepayment rate, which can also be modelled using more sophisticated econometric techniques
St = Servicing fee.
Based on the mortgage balance from the previous month, the above process is repeated.
The link between the months follows the dynamic stock adjustment equation
MBt - MBt-1 = PRt + SPt
Through this equation, the events of one period affect the cash flows of all consequent periods. This is also called path-dependency. Undoubtedly, if it was not for the uncertainty of the prepayments, PRt, the process would be perfectly predictable on the basis of knowledge of i, s, n, and MB0.