Cartesian Graph of Density of Water - Temperature:
Example: The density of water was measured over a range of temperatures. Plot the subsequent recorded data on a Cartesian coordinate graph.
Temperature (°C) Density (g/ml)
40° 0.992
50° 0.988
60° 0.983
70° 0.978
80° 0.972
90° 0.965
100° 0.958
To plot the data the first step is to label the x-axis and the y-axis. Let the x-axis be temperature in °C and the y-axis is density in g/ml.
The further step is to establish the units of measurement along every axis. The x-axis must range from approximately 40 to 100 and the y-axis from 0.95 to 1.00.
The points are then plotted one by one. Below figure shows the resulting Cartesian coordinate graph.
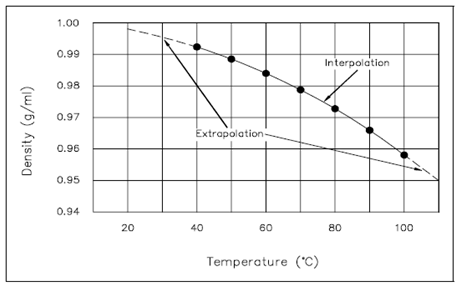
Figure: Cartesian Coordinate Graph of Density of Water vs. Temperature
Graphs are convenient since, at a single glance, the main features of the relationship among the two physical quantities plotted can be seen. Further, if some previous knowledge of the physical system under consideration is available, the numerical value pairs of points could be connected through a straight line or a smooth curve. From these plots, a values at points not specifically measured or calculated can be acquired. In Figures, the data points have been connected through a straight line and a smooth curve, correspondingly. From these plots, the values at points not particularly plotted can be determined. For instance, using Figure, the density of water at 65°C can be determined to be 0.98 g/ml. Because 65°C is within the scope of the available data, it is known as an interpolated value. Also using Figure, the water density at 101°C can be estimated to be 0.956 g/ml. Because 101°C is outside the scope of the available data, it is known as an extrapolated value. While the value of 0.956 g/ml appears reasonable, a significant physical fact is absent and not predictable from the data given. Water boils at 100°C at atmospheric pressure. At temperatures above 100°C it is not a liquid, but a gas. Thus, the value of 0.956 g/ml is of no importance except when the pressure is above atmospheric.
This describes the relative ease of interpolating & extrapolating using graphs. It also points out the precautions which must be taken, namely, extrapolation & interpolation should be done only if there is some prior knowledge of the system. That is particularly true for extrapolation where the available data is being extended into a region whereas unknown physical changes may take place.