Q. Can you explain about Multiple Poles?

Let us consider that F₁(s) has all simple poles except, say, at s = p₁ which has a multiplicity m. Then one can write

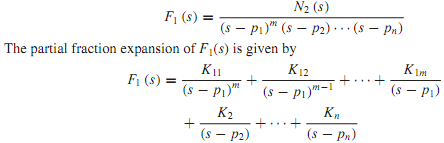
When a multiple root is involved, there will be as many coefficients associated with the multiple root as the order of multiplicity. For each simple pole pk we have just one coefficient Kk, as before.

For simple poles one can proceed as discussed earlier and apply Equation to calculate the residues Kk. To evaluate K₁₁, K₁₂,..., K_1m we multiply both sides of Equation by (s - p )m to obtain

Note that K₂,...,K_n terms play no role in determining the coefficients K₁₁,K₁₂,...,K_1m because of the multiplying factor (s - p1)m in Equation.

The alternate representation discussed for the case of complex poles may also be extended formultiple poles by combining the terms in Equation corresponding to themultiple root. In an expansion of a quotient of polynomials by partial fractions, it may, in general, be necessary to use a combination of the rules given.