Calculated the magnitude of the instantaneous stress:

While a concentrated force of 1 kN is applied at the midspan point of a simply supported beam a static deflection of 5 mm is generated. The same load generates a maximum stress of 158 MN/m². Calculated the magnitude of the instantaneous stress generated when a weight of 10 kg is allowed to fall through a height of 12 mm onto the beam at midspan. What shall be the instantaneous deflection?

Solution                                           

Let We be the equivalent slowly applied load which generates the same static deflection δ_max as that of the impact load.

Then,

We/δmax =      1 kN /0.005 m

= 200 kN/m

Now, equating the work completed by the impact load to that done by the equivalent static load, we obtain

(We/2) δ _max     = W ( h + δ _max )

i.e.

(We /2) × (We/200) = ((10 × 9.81)/1000) (0.012 + We /200)

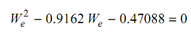
Therefore,

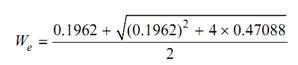
= 0.981 + 0.6932 = 0.791 kN

But

δ _max     = We / 200  = 0.791 /200

= 0.003955 m = 3.955 mm ; 4 mm

 This is given that the load of 1 kN generates a maximum stress of 158 MN/m². Thus, a load of We must produce a maximum stress, σ_max equal to (158 We) MN/m².

∴          σ _max  = 158 × 0.791 = 124.978 MN/m²  ; 125 MN/m²

Therefore, the maximum stress & maximum deflection are 125 MN/m² & 4 mm, respectively.