On a 5-acre level terrain building site, an earthwork contractor has instructed her crew to strip and grub the topsoil of a 60,000-ft² proposed building pad to a minus 2-ft sub-grade and limit the stockpile to 75-ft radius.  The soil has a swell of 40% and an angle of repose at 30°.

The initial height of the stockpile is most nearly:

Solution:

Determine the cubic volume of the cut and the swell of the soil:

60,000-ft² x 2-ft x 1.40 (40% swell) = 168,000-ft³ or 6,222-yd³

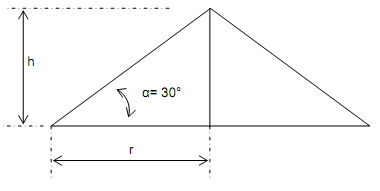
Evaluate the question using the equation for the volume of a cone and the maximum incline of the sides of the cone are at the natural angle of repose equal to the angle of internal friction.  

Check the maximum height based on the natural angle of repose.

r = h ÷ tan α° 

75-ft = h ÷ tan 30°  = h = 43-ft

Using the equation to find the Volume of the cone, solve for h, the Height:  

V = Πr² h/3  

168,000-ft3 = (π 752 h) ÷ 3  

Solve for: h = 28.53-ft is less than the natural angle of repose therefore the solution checks.