Calculate the angular acceleration of the pulleys:

The compound pulley system has a mass of 30 kg and a radius of gyration of 450 mm. Calculate the tension in each cord and the angular acceleration of the pulleys when the masses are released (Refer following Figure).

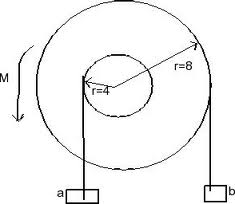
Solution

Free body diagram for the pulley and both the masses are drawn separately as shown in the figure.

We must keep in mind that a₁ = 0.6 α and a₂ = 0.3 α acceleration (i.e. difference in radii). where α is the angular

 Inertial forces are illustrated on FBD. Now, we may write down dynamic equilibrium equations for each of the body.

For a mass of 50 kg, we have

∑ F_y  = 0                     ∴ T₁ - 50 a₁ - 50 × 9.81 = 0

Substituting for a1 in terms of α, we get

T₁  = 50 × 0.6 α + 50 × 9.81

= 490.5 + 30 α  ------------- (1)

For the mass of 150 kg, we have

∑ F_y  = 0                  ∴ T₂  + 150 . a₂  - 150 × 9.81 = 0

∴ T₂  = 1471.5 - 150 × 0.3 α

= 1471.5 - 45 α             ---------- (2)   

For the pulley, we have ∑ M  = 0

∴ 0.6 T₁  + I α - 0.3 T₂  = 0

But       I = 30 × (0.45)²  = 6.08 kg m ²

∴ 0.6 T₁  - 0.3 T₂  = - 6.08 α                  ---------- (3)

Solving Eqs. (1), (2) and (3) as below, we obtain

0.6 T₁  - 0.3 T₂  = - 6.08 α

0.6 (490.5 + 30 α) - 0.3 (1471.5 - 45 α) = - 6.08 α

or,        147.15 = 37.58 α

α = 3.91 rad / sec.

Substituting this value of α in Eq. (1) and (2) above we obtain

T₁  = 607.8 N

and T₂  = 1295.55 N.