A new high temperature alloy has been developed with creep properties as follows: stress exponent, m = 4.5, activation energy, Q = 110,000 J/mol and pre-exponential constant, A = 2×10-8 . The constants A and m are in MPa, % and hour units. Take E = 200GPa for the alloy and the Universal Gas Constant R = 8.314J/molK.
a) In one potential application, the alloy is to be used where it is subject to a constant tensile load of 5kN and service temperature of 800oC and the design allows for a maximum creep strain of 1% over the design life of 10,000 operating hours. (i) Calculate the minimum required cross-sectional area of the blade. (ii) If the temperature were to be increased to 900oC and the load and cross-sectional area kept the same, what would be the time to 1% strain what would the creep strain be after 10,000 hours?
b) In another application, the alloy is to be used for making bolts holding down the flange on a pressure vessel operating at 450oC. The bolts are preloaded to a stress of 400 MPa. (i) Assuming the flange to be rigid, find the time taken for the stress to relax to half the preload value. (ii) Calculate in remaining stress in the bolts after 100 hours.
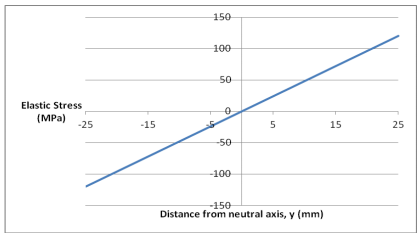
c) For a third application, the alloy is to be used in bending in a component of rectangular cross-section of breadth, b = 20mm and depth, d = 50mm. If a bending moment, M, of 1kNm is applied, the elastic stress distribution across the section, σ = My/I, is as shown in Figure.Using the elastic stress as a basis, sketch the stress distribution across the section if the alloy were to be used at an elevated temperature so that creep is occurring. NB: Only use the positive values of y for your calculations, and sketch the remainder using symmetry.