Calculate force required for equilibrium:

A member ABCD is subjected to the point loads P₁, P₂, P₃  and P₄  as shown in the figure given below

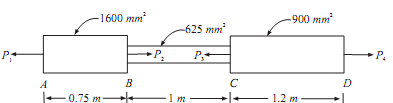
Calculate force P₃ required for equilibrium if P₁ = 120 kN, P₂ = 220 kN and P₄ = 160 kN. Determine the net change in length of member. Take E = 200 GN/m².
Sol.: Modulus of elasticity E = 200 GN/ m² = 2 × 10⁵ N/mm².

By considering equilibrium of forces along axis of the member.

P₁ + P₃ = P₂ + P₄;

120 + P₃ = 220 + 160

Force P₃ = 220 + 160 - 120 = 260 kN

The forces which are acting on each segment of member are shown in free body diagrams shown below:

Let  δL₁,  δL₂ and  δL₃,  be extensions in parts 1, 2 and 3 of steel bar respectively. Then,

 
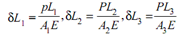
As, Tension in AB and CD but compression in BC,
So, Total extension of the bar,
    
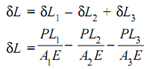
Extension of segment AB = [(120 × 10³) × (0.75 × 10³)]/[1600 × (2 × 10⁵)] = 0.28125 mm

Compression of segment BC = [(100 ×10³) × (1 × 10³)]/[625 × (2 × 10⁵)] = 0.8 mm

Extension of segment CD = [(160 ×103) × (1.2 × 10³)]/[900 × (2 × 10⁵)] = 1.0667 mm

Net change in length of the member = δl =0.28125 - 0.8 + 1.0667 = 0.54795 mm (increase)        .......ANS