Calculate for spring amount of load carried:

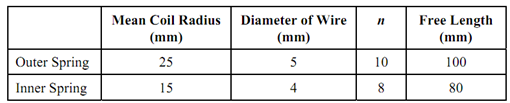
The table below gives specific of a compound spring consisting of two co-axial close-coiled springs. If the spring is subjected to an axial load of 450 N, calculate for each spring

a. the change in length,

b. the amount of load carried, and

c. the maximum shearing stress.

Take G = 80 × 10³ N/mm².

Solution

The free length of outer spring is more than the inner spring by (100 - 80) = 20 mm. Load carried through the outer spring for a deflection of 20 mm is specified by,

Δ= 64 W R³ n / Gd ⁴

⇒ 20 =     64 × W × 25³ × 10 / (80 × 10³ × 54)

∴ W₁  = 100 N

Now the springs are in parallel. Load to be shared by the two springs

= 450 - 100 = 350 N

Δ= 64 W R³ n / Gd ⁴

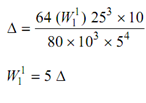----------(1)

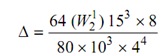
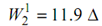       ---------(2)

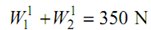
⇒         5 Δ + 11.9 Δ= 350

∴          Δ= 20.7 mm

Change in length, Δ= 20.7 mm

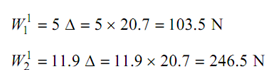
Load taken by outer spring = 203.5 N.

Load taken by inner spring = 246.5 N.

τ _max  =   16 W R  / π d ³

τ_max is outer spring =   16 × 203.5 × 25/( π× 5³) = 207.3 N/mm

τ_max in inner spring =16 × 246.5 × 15/( π× 4³) = 294.2 N/mm

∴ Maximum shearing stress = 294.2 N/mm² (inner spring).