Q. Briefly explain about Laplace transform?
Many commonly encountered excitations can be represented by exponential functions. The differential equations describing the networks are transformed into algebraic equations with the use of exponentials. The operational calculus was developed by Oliver Heaviside (1850-1925) based on a collection of intuitive rules; the transformation is, however, named after Pierre Simon Laplace (1749-1827) because a complete mathematical development of Heaviside's methods has been found in the 1780 writings of Laplace. The Laplace transformation provides a systematic algebraic approach for determining the total network response, including the effect of initial conditions. The differential equations in the time domain are transformed into algebraic equations in the frequency domain.
Frequency-domain quantities are manipulated to obtain the frequency-domain equivalent of the desired result. Then, by taking the inverse transform, the desired result in the time domain is obtained.
The single-sided Laplace transform of a function f (t) is defined by
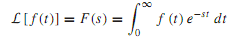
where f(t) = 0 for t< 0, and s is a complex-frequency variable given by s = σ + jω. The frequency-domain function F(s) is the Laplace transform of the time-domain function f (t).When the integral of Equation is less than infinity and converges, f (t) is Laplace transformable.
Note that for σ> 0,e-st decreases rapidly, making the integral converge. The uniqueness of the Laplace transform leads to the concept of the transform pairs,
L[f(t)] = F(s) ⇔ L-1[F(s)] = f(t)
which states that the inverse Laplace transform of F(s)is f (t). It should be noted that the Laplace transform is a linear operation such that
L[Af1(t) + Bf2(t)] = AF1(s) + BF2(s)
in which A and B are independent of s and t, and F1(s) and F2(s) are the Laplace transforms of f1(t) and f2(t), respectively.