Binomial Distribution

Consider a batch of N light bulbs. Each bulb may be defective (S) or non-defective (F). The experiment involves selecting a light bulb and checking whether it is S or F. This experiment is called a Bernoulli Experiment since it has only two outcomes Success and Failure. Suppose it is known that there are M defective light bulbs in the batch. If we represent success by 1 and failure by 0, then

P (Success) = P (X = 1)           = M/N = p (say)

P (Failure)  = P (X = 0)             = 1 - p = q (say)

X is said to be a random variable with Bernoulli distribution.

(Notice that a Bernoulli experiment can always be replicated by a (biased) coin with Head = 1, Tail = 0, P(1) = p)

Suppose the Bernoulli experiment is repeated n times under the same condition. That is, after the light bulb is tested, it is put back into the batch. This way, the probabilities p and q remain unchanged. (This type of sampling is called Sampling with Replacement.)

Let X = Number of successes in n trials.

Then, P(X = x) =

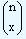px qn - x, x = 0, 1, 2, ..., n  where

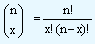We sum up the Bernoulli Process as follows:

1. Each trial has only two possible outcomes.

In our example, the two possible outcomes are whether a bulb is defective or non-defective.

2. The probability of the outcome of any trial remains fixed over time.

In our example, the probability of the bulb being defective or non-defective remains fixed throughout.

3. The trials are statistically independent.

In our example, the outcome of the bulb being defective or non-defective does not affect the outcome of any other bulb being so.

Example

 

Find the probability of getting exactly three heads in 4 tosses of a biased coin, where

P(H) = 3/4 and P(T) = 1/4

P(X = 3)=		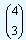(0.75)3 (0.25) = 4 x (0.75)3 x (0.25)
=	0.421875

It can be shown for the Binomial Distribution

m = E(x)  = np s2 = V(X) = npq