Beta of a share
Financial analysts often talk of the beta (b) of a share. We will describe what the beta signifies and the method commonly used to estimate it in this section.
|
Beta of a share is a number that is used to describe how sensitive the share is to the movements in the market as a whole.
|
The market as a whole is represented by a market index such as the Bombay Stock Exchange (BSE), Sensitive Index (Sensex), BSE National Index and Economic Times Index. Suppose, during a period under study, the Sensex has doubled from 900 to 1800, an investor would expect the prices of the shares held by him also to have doubled. Every investor would like the shares held by him to do at least as well as the market, if not better. Whether the individual shares do as well as the market or remain unaffected by the market trends depends upon the sensitivity of stock prices to the market movements. This sensitivity of stock prices to the market movements is measured by beta. If the stock has trebled while the market index has doubled, the stock is considered to be highly sensitive and its beta would be greater than one. If the stock's performance exactly matches that of the market index, the beta of the stock would be equal to one. If the stock's appreciation is only 75% compared to 100% appreciation in market index, then the stock is less sensitive and the beta would be less than one.
Depending upon the beta, shares can also be classified as aggressive and defensive. If the beta of a share is greater than one, the share is classified as an aggressive security. When the market does well, this share will do more than well. Also, when the market takes a downward plunge, shares with beta greater than one would drop in value much faster than the market. If the beta of a share is less than one, the share is classified as defensive security. When the market moves up, the holders of defensive securities would reap less than proportionate benefits. However, when the market moves down, the decline in the defensive securities prices would also be less than proportionate.
Beta is also used to measure the systematic risk of a security. The total risk of a security can be divided into two broad components. The first is the risk specific to the security or diversifiable risk or non-systematic risk. The investor by holding a portfolio which is well-diversified can completely eliminate the unsystematic risk. The systematic risk, which is the second component of the total risk, is that risk associated with the general market movement and it cannot be eliminated through diversification. All securities do not have the same degree of systematic risk because the impact of economy-wide factors could differ from company to company.
Modern Portfolio Theory contends that the required rate of return of a security (which in turn determines the price of the security) depends only on the systematic risk of a security or its beta. The total risk is irrelevant because through diversification, the investor can eliminate the non-systematic risk and hence, the market would not consider the non-systematic risk in the pricing process.
The foregoing discussion brings out the importance of the study of the beta of a security. How is the beta estimated? The returns from a given security are regressed with the return from the market index. The regression line or the line of best fit for the observations is called as the characteristic line. The slope of the line is the beta of the security. While regressing, the return on market index is taken as the independent variable and the return on the security is taken as the dependent variable.
Example
|
Period
|
Return on Market Index (%)
|
Return on Security (j) (%)
|
|
1
2
3
4
5
6
7
8
9
10
|
24
10
36
-16
20
32
14
30
60
50
|
20
12
26
-8
26
28
8
36
48
44
|
|
X
|
Y
|
XY
|
X2
|
|
24
10
36
-16
20
32
14
30
60
50
|
20
12
26
-8
26
28
8
36
48
44
|
480
120
936
128
520
896
112
1080
2880
2200
|
576
100
1296
256
400
1024
196
900
3600
2500
|
|
260
|
240
|
9352
|
10848
|
The characteristic line for the security is 
= 4.24 + 0.76X.
The beta of the security is 0.76.
Since, beta is less than one, the security can be classified as a defensive security.
Once again, we would like to explain the geometric concept of TSS, ESS and RSS.
Consider the graph of the characteristic line.
Figure 20
When x = 30, the value of = 27.04. Note that 
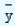= 24. At x = 30, the total deviation of y (= 36) from its mean ( = 24) is 12; of this, the regression line accounts for 3.04 = ( - 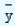). The remaining portion (y - = 8.96) is still unexplained.