Bending moment :

The diagram in created shear forces, but the applied forces also create bending.

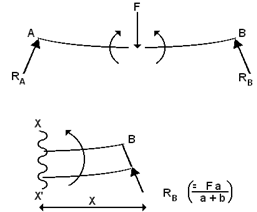
Consider a section x x' at a distance x measured from end B. Then R_B creates a moment about x x', which causes a bending effect.

The Bending moment = R_B . x

As with shear force, moments causing have to be differentiated from moments causing. The first case is +ve bending, the second case is -ve bending.

  is commonly termed "Sagging"
  is commonly termed "Hogging".

Note that as distance x increases, the Bending moment also increases.

Variations in Bending Moment are often shown on a Bending Moment Diagram (BMD).

Considering the beam AB, the BMD is drawn as;

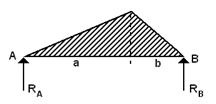
Note that in this case, the BMD is all +ve (i.e. the beam is sagging everywhere) and note also that it increases from zero as x increases to the left of B, up to a maximum and then decreases as the effect of R_B is reduced by the effect of F , finally becoming zero at A.

(Note that BMD can be treated in the same way by considering distances measured to the right of A - the solutions are exactly the same).

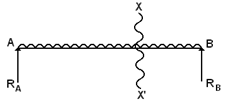
A uniformly distributed load, whilst obeying the same principles, modifies the BMD.

As x increases left of B, R_B causes, but the distributed load also increases and causes .
The BMD now looks like this.

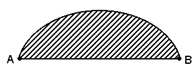
Note: Point loads create BMD's that are triangular. Distributed loads create BMD's that are curved.