Vectors - The Basics

Let us start this section off with a quick discussion on what is the use of vector.  Vectors are utilized to present quantities that have both a magnitude and a direction.  Good instances of quantities that can be presented by vectors are force and velocity.  Both of these consist of a direction and a magnitude.  

 Let us consider force for a second.  A force of like 5 Newtons that is applied in a specific direction can be applied at any point in space.  Alternatively, the point where we apply the force does not alter the force itself.  Forces are not dependent of the point of application.  To describe a force all we need to know is the magnitude of the force and the direction which the force is applied in.

 Similar idea holds more usually with vectors.  Vectors just only impart magnitude and direction. 

They don't impart any type of information about where the quantity is applied.  This is an significant idea to all time remember in the study of vectors.

Graphically vectors are presented by directed line segments.  The direction of the line segment is the direction of the vector and length of the line segment is the magnitude of the vector.  Though, because vectors don't impart any information about where the quantity is applied any directed line segment along with similar length and direction will represent similar vector.

Consider the sketch below.  

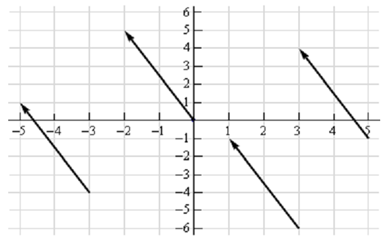
Every directed line segments in the sketch represents similar vector.  In each case the vector starts at a particular point after that moves 2 units to the left and 5 units up. The notation that we'll make use for this vector is,

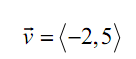
and each directed line segments in the diagram are called representations of the vector.