Average cost function : Now let's turn our attention to the average cost function. If C ( x ) is the cost function for some of the  item then the average cost function is,

                                                  C?( x ) = C ( x ) /x

Following is the sketch of the average cost function  of this equation

 C ( x ) = 2500 -10x - 0.01x² + 0.0002x³

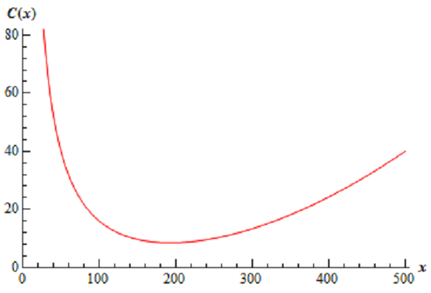
We can notice from this that the average cost function contain an absolute minimum.  We can also illustrate that this absolute minimum will takes place at a critical point with C′ ( x ) = 0 As it clearly will have a horizontal tangent there.

Now, we could obtain the average cost function, differentiate that and then determine the critical point. Though, this average cost function is rather typical for average cost functions therefore let's instead differentiate the general formula above by using the quotient rule & see what we have.

C?′ ( x ) = (x C′ ( x ) - C ( x )) / x²

Now, as we noted above the absolute minimum will take place when C′ ( x ) =0 and it will in turn occur while,

x C′ ( x ) - C ( x ) = 0 ⇒          C′ ( x ) =C ( x ) /x= C? ( x )

Therefore, we can see that it looks like for a typical average cost function we will obtain the minimum average cost while the marginal cost is equivalent to the average cost.

However, we have to note that not all average cost functions will look like it and therefore you shouldn't consider that this will always be the case.