Area between Two Curves

We'll start with the formula for finding the area among y = f(x) and y = g(x) on the interval [a,b].  We will also suppose that f(x) ≥ g(x) on [a,b].

Now we will precede much as we did while we looked that the Area Problem in the Integrals section. We will initially divide up the interval in n equal subintervals all with length,

Δx = (b -a)/n

After that, pick a point in all subinterval, x_i*, and we can then use rectangles on each interval as given here,

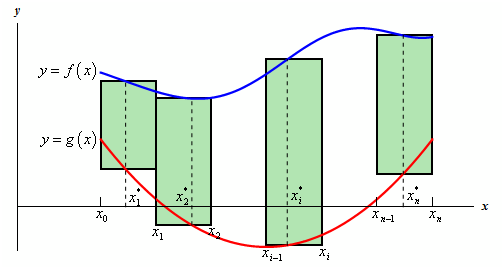
The height of each of these rectangles is specified by,

f(x_i*) - g(x_i*)

and then the area of each rectangle is,

(f(x_i*) - g(x_i*)) Δx

Therefore, the area in between the two curves here is,

A ≈ 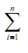(f(x_i*) - g(x_i*)) Δx

So exact area is,

A ≈lim_n→∞ 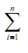       (f(x_i*) - g(x_i*)) Δx

Then, recalling the definition of the definite integral it is nothing more than,

A = _a∫^b f(x) - g(x) dx

The formula beyond will work given the two functions are in the form y = f(x) and y = g(x).  Though, not all functions are in this form. At times we will be forced to work along with functions in the form among x = f(y) and x = g(y) on the interval [c,d] (an interval of y values...)

While this happens the derivation is the same Firstly we will begin by assuming that f(y) ≥ g(y) on [c,d]. We can after that divide up the interval in equal subintervals and build rectangles on each of such intervals. Now there is a sketch of above situation.

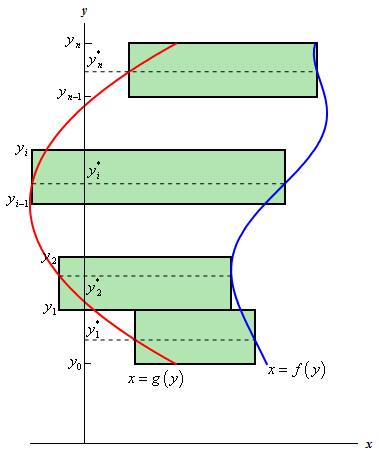
Subsequent the work from above, we'll arrive at the subsequent for the area,

A = _c∫^d f(y) - g(y) dy

Therefore, regardless of the form such the functions are in we use fundamentally similar formula.