Area between Curves

In this section we will be finding the area between two curves. There are in fact two cases that we are going to be looking at.

In the first case we desire to find out the area between y = f ( x ) and y = g ( x ) within the interval [a,b]. We are also going to consider that f ( x ) ≥ g ( x ) .  Take a look at the given sketch to get an idea of what initially we're going to look at.

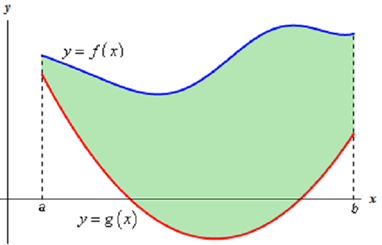
Formula for area in this case

A = ∫^b_a f ( x ) - g ( x ) dx                                               (1)

The second case is almost similar to the first case.  Here we are going to find out the area between x = f ( y ) and x =g ( y ) on the interval [c,d] with f ( y ) ≥ g ( y ) .

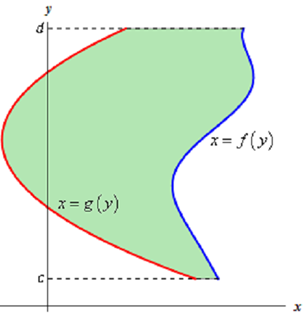
In this case the formula is,

 A = ∫^d_c f ( x ) - g ( x ) dx                                                (2)

Now (1) & (2) are entirely serviceable formulas, though, it is sometimes simple to forget that these always need the first function to be the larger of the two functions.  Therefore, rather than of these formulas we will instead utilizes the following "word" formulas to ensure that we remember that the area is always the "larger" function minus the "smaller" function.

In the first case we will utilizes,

A = ∫^b_a (Upper function) - (lower function) dx   a≤x≤b    (3)

In the second case we will utilize,

A = ∫^d_c (right function) - (left function) dx   c≤y≤d    (4)

By using these formulas will always force us to think about what is going on with each problem and to ensure that we've got the correct order of functions while we go to utilize the formula.