Apply depth-first-search to find out the spanning tree for the subsequent graph with vertex d as the starting vertex.       

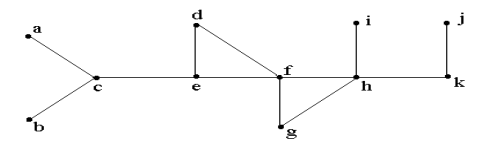
Ans: Let us begin with node'd'. Mark d as visited node. Node'd' comprises two child 'e' and 'f'. After that Visit node 'e' and mark it as visited. Select edge (d, e) and add it to spanning tree T. So, T = {(d, e)}  Now e has e has two children: c and f. Visit c, add (e, c) to T, and mark c as visited. After that visit a and after that b. Mark them visited node and add arcs (c, a) and (c, b) to T. Up to here 

T = {(d, e), (e, c), (c, a), (c, b)}

Now here c has one more child e, which is previously visited, so exit recursion and go up to e that one more unvisited child f. Visit it, mark it as visited and we add (e, f) to T.  f comprise three (3) children: d, g and h. d is visited so leave it. Visit g, and doing the basic work of marking as visited and adding the arc utilized to visit the node in T, we at last get T as 

T = {(d, e), (e, c), (c, a), (c, b), (e, f), (f, g), (g, h), (h, i), (h, k), (k, j)}