Applications of derivatives : At last, let's not forget about our applications of derivatives.

Example   Assume that the amount of air in a balloon at any time t is specified by

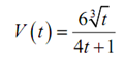
Find out if the balloon is being filled with air or being drained of air at t =8 .

Solution

If the balloon is filled through air then the volume is increasing & if it's being drained of air then the volume will be decreasing.  In other terms, we have to get the derivative so that we can find out the rate of change of the volume at t = 8 .

It will require the quotient rule.

V ′(t ) =  2t ^{(-2/3 )} ( 4t + 1) - 6t ^(1/3) ( 4) /(4t + 1)²

             = -16t ^(1/3)  + 2t  ^(-2/3) / (4t + 1)²

             =  -16t ^(1/3)  + 2/(t^(2/3)) / (4t + 1)²

Note as well that we simplified the numerator more than usual here. It was only done to make the derivative simpler to evaluate.

The rate of change of the volume at t = 8 is then,

V ′ (8) =  -16 ( 2) + (2/4) / (33)²       (8) ^(1/3)  = 2       (8)^(2/3)  = ( (8)^{(1/3 )} )² =(2)² =4

= -  63 /2178= -  7 /242

Thus, the rate of change of the volume at t = 8 is negative and hence the volume has to be decreasing. So air is being drained out of the balloon at t = 8 .