Angle of twist is zero on the shaft:

A shaft 10 m long and 100 mm diameter during its length is fixed at the ends and is subjected to two opposite torques of 8 kN-m and 10 kN-m at a distance of 3 m and 8 m from one end. Discover the fixing torques at the ends. What is the maximum angle of twist and the maximum shear stress in the shaft? At what section the angle of twist is zero on the shaft?

Take E = 80 GPa.

Solution

Σ T = 0

⇒  T_A  - 8 + 10 + T_D  = 0

∴          T_A  + T_D  = - 2

G = 80 GPa = 0.8 × 10¹¹ N/m²              -------------- (1)

d = 100 mm = 0.1 m

 J =  (π /32)d ⁴ = (π/32) × (0.1)⁴  = 9.8 × 10^{- 6} m⁴

R = d /2= 100/2 = 0.05 m ,   Z_P = 1.96 × 10^{- 4} m³

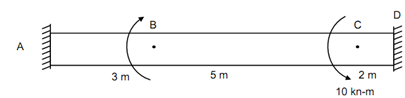
Figure (a)

Figure (b) : Line Diagram

Portion AB

θ ₁ = (T_A . l )/GJ = (T_A × 3 )/GJ                         ---------- (2)

Portion BC

θ₂ = ((T_A  - 8) × 5 )/     GJ               -------- (3)

Portion CD

θ₃ = ((T_A - 8 + 10) × 2)/ GJ = ((T_A + 2) × 2)/ GJ                      ---------- (4)

Angle of twist at D co.r.t A = 0

(T_A × 3 )/ G J + ((T_A  - 8) × 5 )/ GJ + ((T_A  + 2) × 2)/ GJ = 0

∴          T_A  = 3.6 kN-m                                       ----------- (5)

From Eqs. (1) and (5),

3.6 + T_D = - 2

T_D = - 5.6 kN-m = 5.6 kN-m    (  )

Angle of Twist

θ₁ = ((3.6 × 10³ ) × 3) / ((0.8 × 10¹¹ ) (9.8 × 10^{- 6} ))

= 1.4 × 10^{- 2} radians

θ₂ =      ((3.6 - 8) × 10³ × 5 )/(0.8 × 10¹¹ ) (9.8 × 10^{- 6} )= - 2.8 × 10^{- 2} radians

θ₃ =      (3.6 + 2) × 10³  × 2 /((0.8 × 10¹¹ ) (9.8 × 10^{- 6} ))= 1.4 × 10^{- 2} radians

θ_AB  = θ₁ = 1.4 × 10^{- 2} radians

θ _AC  = θ₁ + θ₂  = 1.4 × 10^{- 2} - 2.8 × 10^{- 2} = - 1.4 × 10^{- 2} radians

θ_AD  = θ_AC  + θ₃ = - 1.4 × 10^{- 2}

Shear Stress

 + 1.4 × 10^{- 2}  = 0

τ _max     = (T/ J) . R =  T/ Z _P

Portion AB

τ_max = 3.6 × 10³ / (1.96 × 10^{- 4}) = 18.4 × 10⁶ N/m²  = 18.4 N/mm²

Portion BC

τ _max = (3.6 - 8) × 10³/ (1.96 × 10^{- 4})

= - 22.4 × 10⁶ N/m²  = - 22.4 N/mm²

Portion CD

τ _max      = (3.6 + 2) × 10³/1.96 × 10^{- 6} = 28.6 × 10⁶ N/m²  = 28.6 N/mm²

Zero Angle of Twist

It occurs between B and C

θ₁ = 1.4 × 10^{- 2} radians

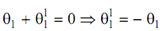
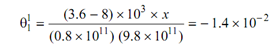
∴ x = 2.5 m from B.