Achieve a perspective projection on the z = 0 plane of the unit cube, demonstrated in Figure (l) from the cop at E (0, 0, 10) upon the z-axis.

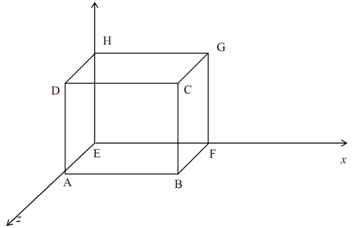
Figure: I

01:  currently center of projection

E = (0, 0, -d) = (0, 0, 10).

∴ d = - 10

We identify here (from equation - 1), the particular point perspective transformation of the projection along with z = 0, plane; here cop is at (0, 0, -d) is provided by:

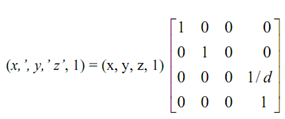
--------------------------(I)

P_n' = P. P_{per, z}                                                                     --------------- (II)

Hence the perspective transformation of a provided cubes v = [ABCDEFGH] to V' = [A'B'C'D'E'F'G'H'] with d = - 10 is provided by:

[V'] = [V] . [P_{per, z}]

Hence the projected points of a provided cube V = [ABCDEFGH] are as:

A' =(0, 0, 0), B' = (1.11, 0, 0), C' = (1.11, 1.11, 0), D' = (0, 1.11, 0), E' = (0, 0, 0) F' = (1, 0, 0), G' = (1, 1, 0) and H' = (0, 1, 0).