Volumes for Solid of Revolution

Before deriving the formula for it we must probably first describe just what a solid of revolution is. To find a solid of revolution we start out along with a function, y= f(x), in an interval [a,b].

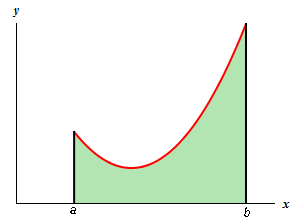
Then we rotate this curve about a specified axis to find the surface of the solid of revolution.  For reasons of this derivation let's rotate the curve regarding the x-axis. Doing that gives the subsequent three dimensional regions.

We require determining the volume of the interior of such object. To do that we will proceeds much as we did for the area in between two curves case.  We will firstly divide up the interval in n subintervals of width,

Δx = (b -a)/n

Then we will select a point from each subinterval, x_i*.

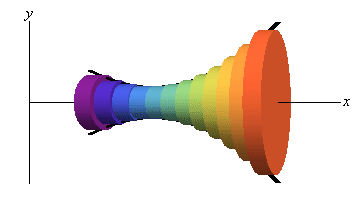
 Here, in the area in between two curves case we approximated the area by using rectangles on every subinterval. For volumes we'll use disks in each subinterval to estimate the area. The area, of the face of each disk is specified by A (x_i*) and the volume of each disk is

V_i = A(x_i*) Δx

Now here is a sketch of this,

Then the volume of the region can be approximated with,

V ≈ 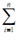      A(x_i*) Δx

Then the exact volume is,

V ≈lim_n→∞ 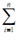       A(x_i*) Δx

= _a∫^b A(x) dx

Therefore, in this case the volume will be the integral of the cross-sectional area on any x, A(x). Consider as well that, here, the cross-sectional area is a circle and we could go farther and find a formula for this as well. Though the formula above is more common and will work for any method of getting a cross section therefore we will leave this like this is.

In the sections where we truly use this formula we will also consider that there are ways of generating the cross section which will actually provide a cross-sectional area which is a function of y in place of x.  In these cases the formula will be as,

V = _c∫^d A(y) dy                                      c < y < d

Here we looked at rotating a curve about the x-axis; though, we could have only as simply rotated the curve about the y-axis. Actually we could rotate the curve about any vertical or horizontal axis and into all of these, case we can utilize one or both of the subsequent formulas.

V = _a∫^b A(x) dx                                      V = _c∫^d A(y) dy