perform a perspective projection on the plane, Computer Graphics

Assignment Help:

Consider at line segment AB in the Figure k, parallel to the z-axis along with end points A (3, 2, 4) and B (3, 2, 8). Perform a perspective projection on the z = 0 plane from the center of projection at E (0, 0, - 2). Also determine vanishing point.

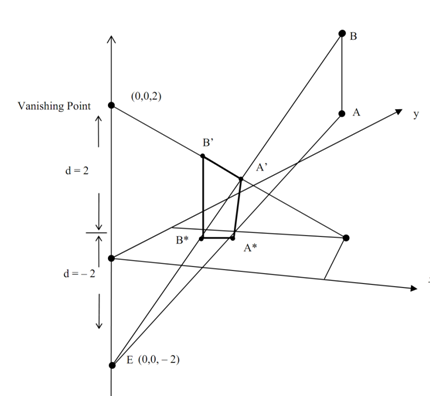
1121_Perform a perspective projection on the plane.png

Figure: (k)

Solution. We know about the Equation (1) shows the center of particular point perspective transformation: of a point P (x, y, z) on z = 0 plane; where (0, 0, - d) is center of projection provided by:

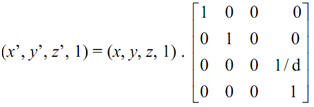
2082_Perform a perspective projection on the plane 1.png

P'_n = P_n. P_per,z ------------------------(I)

Frequently the perspective transformation of provided line AB to A* B* along with d = 2 are as:

V'_n = V_n. P_per,z

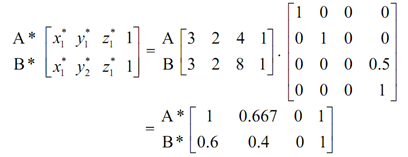
1138_Perform a perspective projection on the plane 2.png

Thus, the projected points of a provided line AB are:

A* = (1, 0.667, 0) B* = (0.6, 0.4, 0)

The vanishing point is given as (0, 0, 0).

Related Discussions:- perform a perspective projection on the plane

Types of animation systems - computer animation, Types of Animation Systems...

Types of Animation Systems - Computer Animation We have discussed above about the sequencing of animation is helpful in developing any animation. Such sequencing is more or le

Gourand shading, what is gourand shading

what is gourand shading

Clipping, 3d clipping

3d clipping

Intensity of colours - raster graphics and clipping, Similarly we can contr...

Similarly we can control the intensity of colours We contain more bit planes for all colour say three bit planes for R, 3 for G and 3 for B here all bit plane of size mxn, hen

Geometric continuity - clipping and 3d primitives, Geometric Continuity ...

Geometric Continuity There is another notion of continuity called geometric continuity. Although the idea existed in differential geometry, the concept was introduced for geome

Rotation - 2-d and 3-d transformations, Rotation - 2-d and 3-d transformati...

Rotation - 2-d and 3-d transformations Given a 2-D point P(x,y), that we want to rotate, along with respect to an arbitrary point A(h,k). Suppose P'(x'y') be the effect of ant

What is 2-dimensional transformation, 2-DIMENSIONAL TRANSFORMATION Mode...

2-DIMENSIONAL TRANSFORMATION Modeling transformation is the mechanism to compose an image from modeling primitives. The modeling primitives are defined in their own coordinate

Polygon rendering, gouroud vs phong

gouroud vs phong

Character genration, what is character genration

what is character genration

Objectives of three dimensional transformations, Objectives of Three dimen...

Objectives of Three dimensional transformations explain basic 3D transformations-translation, rotation, scaling, shear and reflections-applied to objects in space; ex

Write Your Message!

Name

Email id

Message

Verfication Code

User Account

All Pages