We desire to construct a box whose base length is three times the base width. The material utilized to build the top & bottom cost $10/ft² and the material utilized to build the sides cost $6/ft². If the box ought to have a volume of 50ft³ find out the dimensions which will minimize the cost to build the box.

Solution

Firstly, a quick figure (possibly not to scale...).

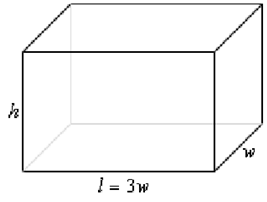
We desire to minimize the cost of the materials subject to the constraint which the volume has to be 50ft³. Note that the cost for each of the side is just the area of that side times the suitable cost.

The two functions we'll be working along with here this time are following,

Minimize : C = 10 ( 2lw) + 6 ( 2wh + 2lh ) = 60w² + 48wh

Constraint : 50 = lwh = 3w² h

We will solve out the constraint for one of the variables & plug it into the cost. It will certainly be easier to solve out the constraint for h therefore let's do that.

                                            h =  50 /3w²

Plugging this in the cost gives,

C ( w) =60w² + 48w ( 50 /3w²)=60w² + 800 /w

Now, let's get the first & second (we'll be requiring this later...) derivatives,

C′ ( w) = 120w - 800w^-2  = (120w³ - 800)/w²         C′′ ( w) = 120 + 1600w^-3

Therefore, it looks as we've got two critical points here. The first is obvious, w = 0 , and it's also just as clear that it will not be the correct value. We are building a box now and w is the box's width and therefore since it makes no sense to talk regarding a box with zero width we will avoid this critical point. However, it does not mean that you have to just get into the habit of avoiding zero while it occurs. There are other kinds of problems where it will be a valid point which we will require to consider.

The next critical point will come from finding out where the numerator is zero.

120w³ - 800 = 0  ⇒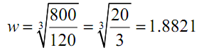      

Therefore, once we throw out w = 0 , we've got a single critical point and now we have to check  that this is actually the value that will give the absolute minimum cost.

In this case we can't utilize Method 1 from above.  Firstly, the function is not continuous at one of the endpoints, w = 0, of our interval of possible values.  Second one; there is no theoretical upper limit to the width which will give a box along with volume of 50 ft³. If w is extremely large then we would just have to make h very small.

The second method tabulated above would work here, however that's going to include some calculations, not difficult calculations, however more work nonetheless.

However, the third method, will work rapidly and simply here.  Firstly, we know that whatever the value of w which we get it will ought to be positive and we can illustrates second derivative above that provided w = 0 we will have C′′ ( w) > 0 and therefore within the interval of possible optimal values the cost function will always be concave up and therefore w = 1.8821 have to give the absolute minimum cost.

All we have to do now is to determine the remaining dimensions.

w = 1.8821

l = 3w = 3 (1.8821) =5.6463

h =  50 /3w² = 50 /3(1.8821)² = 4.7050

Also, although it was not asked for, the minimum cost is: C (1.8821) = $637.60 .