Reference no: EM131976433

Topic: CS and Math

Question: Write the python code for the following problem. Problems are given below.

1. Modified Cholesky Factorization: An n x n positive definite matrix A can be factorized into A = LDL^T, where L is lower triangular and D is diagonal.

Modifications to the diagonal elements of D are applied to ensure that the matrix is "sufficiently positive definite" as follows:

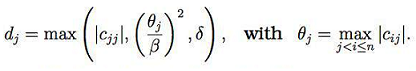
Implement the modified Cholesky's algorithm by integrating the above modification in the appropriate part of the code. Apply your algorithm to the following randomly generated matrix:

import numpy as np

A = np.random.rand(10, 10)*2 - 1

A = A + A.T

Quantify the difference between A and the modified version A, as outputted by the algorithm by 1) comparing the eigenvalues of the two matrices; 2) comparing the diagonal values of the two matrices, and 3) computing the sum of the squares of the non-diagonal elements of A - A_m. Use appropriate scipy functions for eigenvalue and norm computations as needed. Use δ = 10^-8 and β = 100 in your implementation. Comment on your results.

2. Steepest Descent with quadratic interpolation line search: Consider the usual steepest descent step x_k+1 = x_k + α_kp_k, where α_k is the step size and p_k = -∇f(x_k). During the k-th iteration of the steepest descent algorithm, we first make and initial guess α₀ for the step-size as:

α₀ = (2(f(x_k) - f(x_k-1)))/φ'(0),

where φ(α) = f(x_k + αp_k). Performing a quadratic interpolation using φ(0), φ'(0), and φ(α₀) as knot points and minimizing the quadratic, we obtain the new trial step

α1 = φ'(0)α₀²/(2[φ(α₀) - φ(0) - φ'(0)α₀]).

If the sufficient decrease condition:

φ(α) ≤ φ(0) + c₁αφ'(0)

is satisfied, we terminate the search, Otherwise, we use φ(0), φ'(0), and φ(a₁) as new knot points and continue the search. Write a python program using the TensorFlow package to implement this approach. Apply your implementation to minimize the Rosenbrock function and benchmark the required number of iterations to converge to the minimum [within 10^-6 tolerance) against the built-in method GradientDescentOptimizer () with constant learning rate 0.001. Use c₁ = 10^-4 in your implementation.

3. Conjugate Gradient (CG): Let A be n x n positive definite matrix. Implement the CG method for solving the linear system Ax =b as outlined in attached file.

Apply your algorithm to solve a linear system in which A_i,j = 1/(i + j - 1) and b = (1, 1, · · · , 1)^T. Set the initial point x₀ = 0 and try dimensions 5, 8. Report the number of iterations required to reduce the residual below 10^-6. Verify your solutions by comparing your results with the builtin scipy solver.

Attachment:- Assignment File.rar