Reference no: EM132194609

Problem 1

Consider the following circuit. Assume V_γ = 0.7V, R₁ = 1kΩ, R₂ = 1kΩ, VDC = 2V.

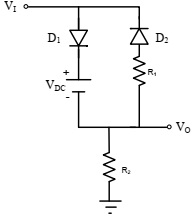
Plot VO versus V₁ for -5V < V₁ < 5V.

Problem 2

Consider the following circuit with R₁ = 40kΩ, R₂ = 60kΩ, R_L = 5kΩ, R_E = 1kΩ, R_S = 4kΩ, β = 100, V_A = 100V, V_BE(ON) = 0.7V, V_T = 0.026V.

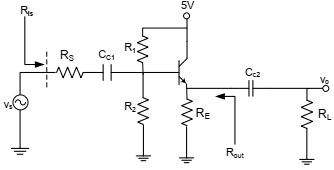
a) Determine the Q-point (IC, VCE)
b) Draw the small-signal equivalent circuit and determine Ris and Rout
c) Determine the voltage gain.
d) Draw the dc and ac load lines and determine the maximum symmetrical output voltage swing.

Problem 3

Consider the following circuit. V_DD = 15V, R₁ = 600kΩ, R₂ = 400kΩ, R_L = 20kΩ, R_D = 2.5kΩ, R_S1 = 100Ω, R_S2 = 900Ω, Kn = 1mA/V², V_TN = 1.5V, λ = 0.

a) Determine the Q-point.
b) Draw the small signal equivalent circuit.
c) Determine the voltage gain.
d) Determine Rin and Rout

Problem 4

Consider the following circuit. Assume V_TN = 1.0 V, Kn = 1 mA/V², λ = 0, V⁺ = 5V, V^- = -5V, R_L = 5kΩ, R_Si = 5kΩ, R_G = 600 kΩ.

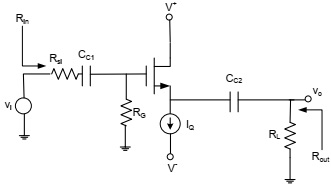
a) Draw the small signal equivalent circuit
b) Write the expression for the voltage gain.
c) Determine IQ such that Av = 0.9
d) Determine Rin and Rout
e) Determine VDS and VGS.

Extra Credit

Consider the following circuit. Assume V_γ = 0.7V, V_B = 3V. Assume the RC time constant to be much larger than the period of the input signal.

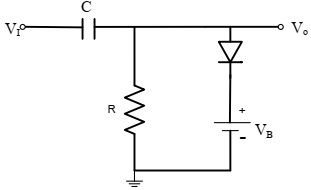
Plot the steady-state V_o as a function of time for V_I = 10 sin (1000t) V.