Reference no: EM133109976

MAE 3319 Dynamic Systems Modeling and Simulation

A simple schematic for a pneumatic lift system with automatic speed reduction is shown below. Initially, the lift is descending with a constant speed of 3 m/s forcing compressed air through a valve at the bottom of the cylinder. At y = 4 m, the flow area of the valve at the bottom instantly decreases by 75% reducing the air flow through the valve and thus, slowing down the descent of the lift.

The objective is to simulate the dynamics of the lift system out to about 15 s or until the piston reaches the bottom of the cylinder. Particularly, we want a plot of the normalized displacement of the mass y(t)/y(0-), a plot of normalized speed y? (t )/ y? ¿ and a plot of the normalized pressure in the cylinder P(t)/Patm all three on the same graph with a legend.

The total mass of the piston and mass being lowered is M = 125 kg. The pressure on top of the piston is vented to atmosphere. Gravity is g = 9.81 m/s². The steel cylinder inside diameter is nominally Di = 0.1 m and the outside diameter is nominally Do = 0.106 m. Assume the steel cylinder is rigid; that is, the diameters don't change during the simulation; so, the only volume change during the simulation is due to the piston movement (Section 5.3.1).

 

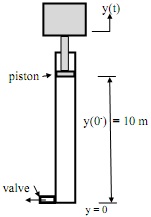
(a) If the speed is constant prior to the valve area changing, what is the gage pressure in the cylinder prior to the valve area reduction? Show that this pressure is 0.415e5 N/m² gage.

Hint, start with the force balance on the mass. Using gage pressure P for the gas and assuming there is viscous friction associated with the piston rubbing the cylinder wall; use 300 y? friction force. for this

(b) Add Patm = 1e5 to the pressure obtained in (a) to make it absolute. Assuming the initial m² temperature of the air in the cylinder is 275 K and the gas constant for air is R = 286.8 , use K s² the ideal gas equation to show that the initial density of the air in the cylinder 1.8 kg/m3. See Section 5.3.1.

(c) Using the initial speed of the mass and the density found in (b), use the conservation of mass equation to show that the initial mass flow rate through the valve prior to the valve area reduction is 0.042 kg/s. Is the air leaving the cylinder or coming into the cylinder?

(d) Assuming the pressure on the downstream side of the valve is atmospheric, determine if initially the flow through the valve is choked or unchoked. (Section 5.5.3)

(e) Based on your answer in (d), use the orifice equation for the valve to show that the valve flow area Ao is initially Aoi = 0.000147 m2. Assume the discharge coefficient is 0.9 and the specific heat ratio for air is 1.4. See Section 5.3.3.

(f) Show that the valve area Ao after a 75% reduction is 0.0000368 m².

(g) Write the capacitance equations for the fluid in the cylinder. Assume the cylinder volume under the piston is V = Ay + 0.01. See Section 5.3.1. Note, 0.01 has been added to avoid dividing by zero when y is very close to zero.

For the pressure in the cylinder:
For this simulation, assume that it happens so fast that there is little if any time for heat transfer and thus, use a small value for r such as 0.2.
For the density in the cylinder:
For the changing temperature in the cylinder:

(h) Write the conditional orifice flow equations for flow through the valve. Assume that the pressure P never drops below Patm due to the mass bouncing causing air to be sucked back into the cylinder (reverse flow).

(i) Since the force balance equation is 2nd order and there is a 1st order equation for the pressure and a 1st order equation for the density, to simulate this system, we need 4 state variables and a numerical integration algorithm since this is a nonlinear system. Generate the normalized plots mentioned in the introduction to this homework. Run the simulation for 15 s or until an event function (Section 2.8.6.3.3) stops it when y decreases to zero. See examples in Section 5.3.3.
(3%) Confirm that your speed remains constant until Ao starts decreasing.

(j) On your plots in (i), use ‘datatips' to identify pressure and speed levels at the times of valve area reductions. Also, identify the peak pressure and the minimum speed prior to y reaching zero. Also, insert a horizontal line denoting the transition from choked to unchoked flow. Note, 1/0.52828 = 1.89