Reference no: EM131038876
Consumer Theory
1. The Ministry of Infrastructure in a developing country has an annual budget of £m this year and has to allocate it among construction of roads (x1= km of roads built during a year and also includes maintance works) and the expansion of the port capacity (x2 = extra tons that can be transported from/to the port after the expansion). Each ton of capacity added to the port costs £p2. However, each ton of extra capacity in the port will increase the number of trucks in the roads and this will be reflected in the annual cost of the road construction.
The calculation of the cost of each km of roads includes: Cost of building the road (Lb per km of road) and the repair/maintenance cost which depends on the number of trucks using it (this cost is £g * (Number of trucks)) per km of road). The ministry estimates that every ton of capacity added to the port will attract 10 extra trucks to the road system (i.e. the number of trucks using the roads will be equal to 10 * x2). Note that the maintenance of roads built in the past are not included in any calculation because a private company operates them.
(a) Write the Budget Constraint of the ministry as a function of the annual budget m, the km of roads x1, the added tons to the port x2, and the costs p2, b and g.
(b) Represent this budget line in the space x1, x2 (assume some positive values for g,pi,p2, b and m if it helps you to draw it). Can you see any difference from the case studied in class?
(c) What can you say about the opportunity cost of expanding the port capacity? Is this intuitive for you? How can you explain in words this phenomenon?
2. A car manufacturer is studying the characteristics of the typical consumer in the car's market, he wants to understand the preferences of this consumer for "comfort" and "power" in a car. He implements a consumer survey and concludes that the preferences of a typical consumer can be well approximated by the utility function u = x10.5 x20.5 where x1 is the degree of comfort of the car and x2 is the power of the car's engine (measured in horsepower units). In this setting, a bundle is a car with a particular combination of comfort and power. For instance, a bundle (30,25) is a car with 30 units of comfort and 25 units of power.
(a) Rank the following combinations (or bundles) of comfort and power in a car for this typical consumer: (30,25), (40,10), (256,9), (20,35), (10,15), (36,64).
(b) Assume the consumer buys a car with 64 units of x1 and 81 units of x2.
i. The manufacturer is considering a different version of the car with a bit more of comfort. Can you measure how much is the consumer willing to reduce the power of the engine without complaining about the change?
ii. How does your answer to i) change if the bundle is (256, 9) instead of (64,81)? Which characteristic of preferences can explain this result?
(c) The firm is considering a new sale strategy: it will allow consumers to choose their preferred combination of power and comfort, i.e. the consumer can "personalize" his car. The "price" the firm would charge per unit of confort is pi and the "price" charged per unit of power is p2. Can you predict the characteristics of the car that a consumer with incomeLm will choose? (your answer should depend generically on the values of pi, p2 and m)
3. You have invested in shares from a large electronic company from a country X. You can assume that there are two large groups of goods in that country. Electronic goods (x2) and a group of commodities that includes food, clothes and transportation (xi). The government announces that will eliminate the actual taxes imposed on x1 goods. Should you buy more shares of the electronic company or should you sell your stock? Is there any characteristic of x1 that could make you more confident about buying more shares of the electronic company? Illustrate your answer with a diagram/s. (Hint: Think in the Slutsky decomposition)
Production Theory and Market Structure
1. For this question you must use diagrams where the horizontal axe is units of labor and the vertical axe is units of capital.
(a) Show that in the short run (when capital level is fixed at some level) the total cost of producing any level of output is higher than the long run total cost of producing the same level of output. This is true for any level of capital except from one level where both costs are similar.
(b) Show that a decrease in wages will reduce the total cost of a given level of output more in the long run. Assume now that you can't expand the level of capital (for example capital = plant size) but you can interrupt the ongoing contracts for free and use less capital. Does your answer change in that case?
2. Is the DWL of a tax higher when the demand is more elastic or when it is less elastic? (Hint: Assume that the supply is flat and compare two linear demands with different elasticity but the same initial equilibrium, you will be comparing two triangles of similar height) Can you give some intuition for this?
3. The fast growth of a city has increased the interest for building a high speed railway connecting it with the capital. A recent survey on potential travellers has shown that there are two group- of travellers: 2000 individuals with a daily demand (each traveller) xd(p) = 1/4 - 3/2000p and 1000 travellers with daily demand (each traveller) xd(p) = 1-6/1000 p where p is the ticket price for one trip
Most of the costs involved in the building and operation of the railway are the following (for convenience expressed in £ per day):
- Loan repayment of invested capital = £7000 per day
- Wages for employees (independent of trips) = £8000 per day
- General maintenance, not related with trips =L3000 per day
- Wages of drivers and crew workers (related to number of tickets) = L1 per day (per ticket)
- Maintenance costs related with use = The cost of one passenger increases linearly with the number of passengers, every passenger in a trip costs L0.1 more than the previous one (i.e. the maintenance cost of one ticket is 0.1x where x = number of sold tickets)
Assume that 10 firms decide to build a different railway each and that they will behave as in a competitive market, i.e. they take the price of the market as given and decide how many tickets per day are sold (Their decision is basically how many trips a train will complete during a day, thus they can save wages and maintenance cost related with trips but not fixed costs)
(a) Obtain the market demand for train tickets
(b) What will be the profits/losses of the firms in this competitive environment?
(c) Assume now that goverment only allows one firm to enter the market, but the firm is free to choose the price of tickets.
i. What price will this firm charge per ticket? Calculate the profits of the firm
ii. Calculate (if any) the social cost of allowing only one firm operating in the market. Interpret intuitively.
(d) The government decides that trains should be accessible for a larger number of people and imposes a maximum price such that the firm makes normal profits.
i. Calculate this price (Hint: it can be useful to express profits as a function of price)
ii. Now suppose that the government forces the monopolist to provide a quantity such that the price equals the marginal cost. Will the monopolist remain in the market without a subsidy?
Game Theory
1. Answer the following questions
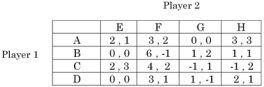
(a) Find the NE in pure strategies of the following game
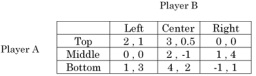
(b) Find the Nash Equilibria in pure and mixed strategies of the following game. Explain your answers and how you obtain it. (Hint: Given that players are rational, is there any way of making the game simpler? revisit lecture slides for more hints)
2. Find the equilibria of the following game: Two players pick simultaneously a number between 0 and 1 (they can choose any rational number in this interval). Call these numbers Sa and Sb respectively. Then, they add the numbers and divide by four, i.e. (Sa + Sb)/4. The player who submitted the number closest to (Sa + Sb) /4 wins £200 and the other wins nothing, if they submit the same number, they receive £100 each. Find the Nash Equilibrium of this game.
3. Two politicians (A and B) must decide their political platforms. Candidates only care about wining the election. Imagine that voters are evenly distributed in a scale from 1 to 100 where 1 is extreme left and 100 is extreme right. An individual always vote for the candidate closer to his political position. If the two candidates are at the same "distance" from a citizen, she toss a coin to decide her vote (if many individuals are at the same distance to both candidates, you can expect that half of them will vote for A and half for B). If candidates get the same number of votes, the winner is decided by the congress where both candidates A have the same probabilities of being chosen. Call PA and Pk; to the political positions chosen by candidates (e.g. PA = 1 means that candidate A's platform is extreme left, etc).
You should provide some intuition but also the fomal aspect is important (How you specify the NE, strategies, etc. is important as well). Consider only pure strategies.
(a) What is the Nash Equilibria of this game if candidates decide simultaneously? Is there a unique NE or multiple NE? Does the winning-at-congress probabilities matter for candidates in this game (e.g. what happen if these probabilities are 0.1 and 0.9) ?
(b) Assume that candidate A must announce his platform some time before candidate B. What is the SPE of the game? (For the formal answer, remember the definition of strategies in dynamic games)
(c) Now assume that there are three candidates instead of two and they decide simultaneously. Find the Nash Equilibrium or explain if there does not exist a NE. For simplicity assume that candidates just try to maximize the number of votes.
4. Consider the Cournot Dupoly model. The demand of the market is P = 100 - 2Q. Firm A has a total cost function CA(qA) = cAqA and firm B has a total cost function CB(qB) = cBqB where cA and GB are two real numbers < 10
(a) Find the Nash Equilibrium of the game. Show that an increase in the own marginal cost has a larger impact in the produced quantity than an increase in the competitor marginal cost. (15 marks)
(b) Now assume that CA(qA) = 4qA and CB(qB) = 64+ 16q2B but firm A decides first. Assume that firms are deciding in the long run. What is the SPE of the game? Can you find a NE that is not SPE in this game? Is that equilibrium sequentially rational? (Hint: Don't proceed mechanically with Stackelberg model, think in the last stage a bit more and analyze what firm B should do in different scenarios)