Reference no: EM132493593

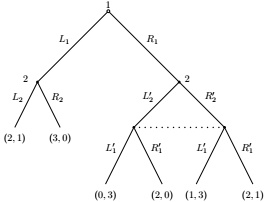
Question 1. Solve for all Nash equilibria and all subgame-perfect Nash equilibria of the two-player game shown below.

Question 2. Consider the following three-player normal-form game. Player 1 chooses x ∈ R₊, player 2 chooses y ∈ R₊ while player 3 chooses z ∈ R₊. Payoffs are given by

u₁(x, y, z) = 2xz - x²y, u₂(x, y, z) = 12(x + y + z) - y, u₃(x, y, z) = 2z - xyz².

Solve for all (pure and mixed strategy) Nash equilibria of the game.

Question 3. Consider a simplfied version of infinitely-repeated Bertrand price competition where two firms must choose prices for the month (p₁, p₂). We will consider two prices: a collusion/monopoly price p_M and a lower competitive price of p_C. The game between the two firms is given by

where π_M is the total profits available if the two firms successfully collude. The discounted sum of profits given a sequence of monthly prices (p₁^t, p₂^t )^∞_t=1 is given by

∞   1 2 t=1
∑  δ^t-1π_i(p₁^t, p₂^t )
t=1

(a) Write out the discounted-average sum of profits.

(b) Draw the set of feasible discounted-average profits of the repeated game.

(c) So long as δ is close enough to one, how does the set of payoffs supportable as a Sub-game Perfect Nash Equilibria (SPNE) differ from the set of feasible payoffs?

(d) Draw a diagram representing a one-period punishment strategy where both firms choose the price pM but switch to play pC one time on any deviation, and then return to trying to collude. What are the conditions on δ for the strategy you outlined to be a sub-game perfect Nash Equilibrium?

(e) Suppose that δ = 3 . Are there other strategies that might work to support collusion as an SPNE?

Question 4. Consider an auction with two bidders, i and j, and in which bidder i's type is an element ti [0, 1]. Both bidders value for the good is v = t1 + t2, so it is the sum of their types. However, a player only utility v(t) p, where p is the second highest submitted bid, and losers have utility zero. Assume knows his own type, not his opponent's. The format is a second-price auction, so that the winner has throughout that types are independently and uniformly distributed.

(a) Define the notion of a bidding strategy and the notion of a symmetric Bayesian Nash equilibrium for the second-price auction.
competitor has a type tj ≤ ti. What is the conditional expectation in the special case ti = tj? (b) Compute the expected value of the object for a bidder with type ti and the information that his
(c) Suppose that the bidders use symmetric strategies. Let β(t_i) denote the bid of player i when her type is ti and let α(b) be its inverse. Show that i's payoff from bidding b can be written as

α(b) (ti + α(b)/2) ₀∫^α(b)β (tj) dtj

(Hint: Use the insights from the conditional expectation obtained in part b).

(d) Derive the symmetric Bayesian Nash equilibrium with two bidders.