Reference no: EM132909514

Question 1. Find the function of the form
y = c₀ + c₁ sin(x)
that best fits the data in the following table in a least squares sense; that is, minimize
4
∑(y_i - c₀ - c₁ sin(x_i))².
i=1

i	xi	yi
1	0	1
2	Π/2	2
3	Π	0
4	3Π/2	-2

(a) Set up the least squares problem to be solved in the form Ax ≈ b. (b)(6 points) By hand, find the reduced QR factorization of the matrix in part (a) and use this to solve the problem. Show your work and leave square roots as square roots (that is, do not approximate them with decimal numbers).

(c) Write down the normal equations and make sure that the solution you found in part (b) satisfies these equations.

Question 2. Let

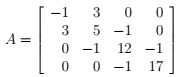
(a) Sketch the Gerschgorin row disks and indicate how many eigenvalues of A lie in each region.
(b) Let D = diag(1, 1, 1, d), d > 0. Then

For what value of d will the Gerschgorin row disks give the sharpest information about the eigenvalue near 17, and how close to 17 will they show it to be? Explain your answer.

Question 3. Suppose A has four eigenvalues: 2, 0, 1, and 3. What range of shifts (if any) can be used with the power method to make it converge to an eigenvector corresponding to the eigenvalue 1? What range of shifts (if any) can be used with inverse iteration to make it converge to an eigenvector corresponding to the eigenvalue 1? Explain your answers.

Question 4. Let A be a real symmetric 2 by 2 matrix with eigenvalues λ₁ = 1 and λ₂ = 2 and with corresponding orthonormal eigenvectors ^→q1 and ^→q2. Let s = 1 + 10^-15.
(a) What is the 2-norm condition number of A - sI?
(b) About how many (decimal) digits of accuracy would you expect in the computed solution to a linear system of the form (A - sI)^→x = ^→b, if you solve it using a backward stable algorithm on a machine with unit roundoff smachine approximately equal to 10^-16?
(c) Suppose your computed solution ^x is the exact solution to (A-sI)x^ = ^→b + 10^-16(^→q1 + ^→q2). Express the error x^ - ^→x as a linear combination of ^→q₁ and ^→q₂. Which component is larger?

[This is why shifted inverse iteration converges in practice. The linear systems are not solved very accurately, but the error is in the direction of the eigenvector that we are seeking!]

Question 5. A student is taking exams. His answers are either right or wrong and as soon as he enters an answer he is informed whether it is right or wrong. If he gets a question right, his confidence grows and his probability of answering the next question correctly is 0.9. But if he gets a question wrong, his confidence goes down and his probability of answering the next question correctly is only 0.6. If he answers many, many questions, under these conditions, what percentage do you expect him to get right? Does it depend on whether he gets the first question right or wrong? Write down the states of this system and the probability transition matrix, and explain how you get your answer.

Question 6. Let

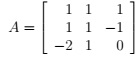
Note that the columns of A are orthogonal but not orthonormal.
(a) Write down the SVD of A. [Leave square roots as square roots and explain how you get your answer; you may use Matlab to check it if you like, but do not simply write down a result from Matlab.]
(b) Write down the closest (in 2-norm) rank 1 approximation to A.

Question 7. Let A be an n by n matrix, and suppose that the right and left singular vectors ^→v1 and ^→u1 associated with the largest singular value σ1 of A are orthogonal to each other: ^→uT ^→v1 = 0. Show that for every real number t ≠ 0,

||A + tI||₂ > ||A||₂

Attachment:- matrix.rar