Reference no: EM132014092

Advanced Mechanics of Solids Assignment -

Question 1 - Note: - Attempt any eight questions from Question 1.

i. Write down the generalised Hooke's law for isotropic material in matrix form.

ii. Define anisotropic material with examples.

iii. Write down the formula for normal stress and shear stress in terms of lame's coefficient λ and μ.

iv. Define shear centre.

v. Write down St. Venant's assumption.

vi. Differentiate between symmetrical and unsymmetrical bending.

vii. Write the Euler-Bernoulli equation for bending of beams.

viii. Indicate the flow of distribution of shear stress due to transverse shear and shear centre location for a thin walled inverted T section.

ix. Write the formula for Young's modulus E and Bulk modulus K in terms of lame's coefficient λ and μ.

x. On which factors, location of shear centre depends?

xi. Write down the Winkler-Bach formula for bending of curved beams.

xii. Compute Lame's coefficient λ and μ for steel having E = 207 x 106 kPa (2.1 x 106 kgf/cm2) and ? = 0.3.

Question 2 - Derive Winkler - Bach formula to find bending stresses in initially curved beams.

OR

Question 2 - A cantilever beam of rectangular section is subjected to a load of 2000 N which inclined at an angle of 60^o to the vertical as shown in figure. Determine the stress due to bending at appoint A near the built in end.

Question 3 - For steel, the following data is applicable:

E = 207 x 10⁶ kPa (2.1 x 10⁶ kgf/cm²)

and G = 80 x 10⁶ kPa (0.82 x 10⁶ kgf/cm²)

For the given strain matrix at a point, determine the stress matrix.

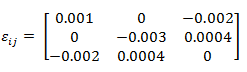
OR

Question 3 - Derive the Lame's displacement equations of equilibrium.