Reference no: EM132760971

Solve the following problems.

Question 1.
Explain in words and/or formulae the followings concepts:
(a) A square matrix A is invertible.
(b) A rectangular matrix A is a full column rank.

Question 2.
(a) Give an example of a set of vectors that is orthogonal with respect to the Euclidean inner product on R², but is not an orthonormal set.
(b) Give an example of a set of vectors that is orthonormal with re-spect to the Euclidean inner product on R².

Question 3.
(a) Write down the augmented matrix for the given system of linear equations:
x+2z =5,
x+y-z=3,
2x - y = 1.
(b) Solve the linear system by Gauss-Jordan elimination.
(c) Solve the system by Cramer's rule.

Question 4.
Let X be any m x n full rank matrix (m < n). We define the Hat matrix as H = X(X^T X)^-1X^T . Hat matrices play an important role in multiple linear regression models.
(a) Show that the Hat matrix is symmetric and idempotent.
(b) Show that the Hat matrix is invertible only if H = I.

Question 5.

(a) Determine the ranks of the following matrices (for square matri-ces use WolframAlpha/Excel to check their determinants: if the determinant is zero, remember that the matrix can not be of full rank; also remember that row rank = column rank for rectangular matrices).

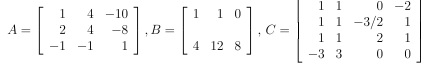
(b) What matrices in (a) are full column rank?

(c) For those matrices in (a) that are not of full column rank, show that at least one column is a linear combination of the others by finding α and β (not both zero) so that α x c1 + β x c₂ = c₃ where ci respectively a column of the matrix.

(d) Show that the rows of C are orthogonal to each other but that the first two columns are not orthogonal.

(e) Suppose now we rescale the rows of C so that each row is a unit vector (i.e. a vector of unit length). In other words we multiply each entry of a row by a number a such that sum of squares of the rescaled row becomes 1; of course a may differ from row to row. Let E be the matrix whose rows are the rescaled rows of C. Write out E.

(f) Show that the columns of E are also orthogonal.

Question 6.

Let (u, v) be the Euclidean inner product on R² and let u (-3, 2), v = (1, 1) and k = -2. Solve the following questions.
(a) (u, v)
(b) HO
(c) The distance between the two vectors: d(u, v).
(d) llu - kvil.
(e) Are u and v linearly independent in R²? Show your reasoning.
(f) Show that the set of vectors {u, v} is a basis in R2.

(g) Use the Gram-Schmidt process to transform the basis {u, v} into an orthonormal basis {w₁, w₂}.
Question 7.
Find:
(a) the least squares straight line and
(b) the least squares quadratic polynomial
that best fit the four points (0, 0), (-2, 1), (1, -2), (4, 4). You can use WolframAlpha or other software to solve matrix operations, but not to find the solutions. Show your complete reasoning.
[Hint: In both cases you need to solve the equation y=Mv where y and v are vectors and M is a matrix.

Question 8.
(a) By solving the characteristic equation, determine the eigenvalues of the matrix
[ 2 -3 A = 1
1 -2
(b) Determine the eigenvectors associated with the eigenvalues found in part (a).
(c) Rescale the two eigenvectors to be vectors of unit length and write out the spectral decomposition of A.

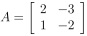
Question 9.
(a) Show that the following matrix is diagonalizable

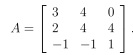
(b) Then find a matrix P diagonalizes A.