Reference no: EM132449423

Problems -

Problem One: Imagine an infinite line of charge of charge with charge per unit length -λ. Surrounding the line of charge is a cylinder of inner radius a and outer radius b. The cylinder has a volume charge density αr. The permittivity of free space is ε₀. Answer the following in terms of quantities given or a subset thereof. Use Gauss' law.

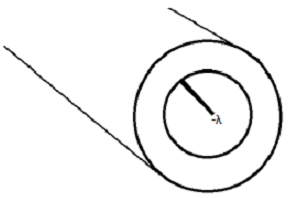
(a) What are the units of α?

(b) What is the electric field for r < a?

(c) What is the electric field for a< r < b?

(d) What is the electric field for r > b?

Problem Two: In the diagram below a point charge -Q is at the origin. It is surrounded by a spherical conducting shell of inner radius a and outer radius b. Answer the following in terms of quantities given or a subset thereof

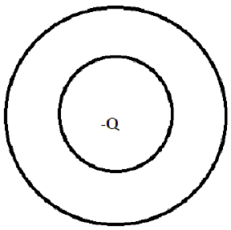
(a) What is the electric field for r < a?

(b) What is the electric field for b > r > a?

(c) What is the electric field for r > b?

(d) Plot the magnitude of the electric field everywhere.

Problem Three: In the diagram below the inner sphere has radius a and charge per volume αr. The outer where has radius b and charge per volume γr². Use Gauss' law to answer the following.

(a) What are the units of α?

(b) What are the units of γ?

(c) What is the electric field for r < a?

(d) What is the electric field for b > r > a?

(e) What is the electric field for r > b?

(f) Plot the magnitude of the electric field everywhere.

Problem Four: Electric charge is distributed non-uniformly along a thin rod of length a, with total positive charge Q, whose charge density λ(x) is a function of x given by λ(x) = Ax³. A is positive constant.

a) Find the electric field at point P, a distance L to the right of the rod. Give your answer in terms of a, Q, L, and known constants. Take the origin of your x-axis at the left end of the rod.

b) What does your result for the electric field reduce to as L becomes much larger than a (but not infinity)?

Problem Five: Consider the following circuit, consisting of batteries and resistors:

a) Write down the applicable Kirchoff equations for the currents at each junction.

b) Also write down the applicable Kirchoff equations for each loop.

c) Solve these equations for each current indicated in the figure.

d) Determine the voltage drop across each resistor.